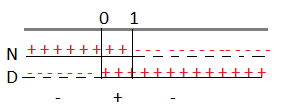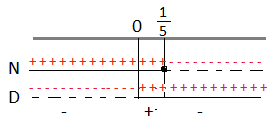Esercizi sulle disequazioni fratte

Pubblicato il da ImpariamoInsieme

 

Esercizi sulle disequazioni fratte

Esercizio n° 1

Risolvi la seguente disequazione numerica fratta.

\frac{2x + 3}{4x + 4} – 1 ≤ \frac{x - 1}{x + 1}

Esercizio n° 2

Risolvi la seguente disequazione numerica fratta.

\frac{1}{x } < 0

Esercizio n°3

Risolvi la seguente disequazione numerica fratta.

\frac{1}{x-1 } > 0

Esercizio n° 4

Risolvi la seguente disequazione numerica fratta.

\frac{x+1}{x} > 0

Esercizio n° 5

Risolvi la seguente disequazione numerica fratta.

\frac{1 - x}{2x} ≥ 0

Esercizio n° 6

Risolvi la seguente disequazione numerica fratta.

\frac{3x - 6}{2x + 1} ≥ 0

Esercizio n° 7

Risolvi la seguente disequazione numerica fratta.

\frac{5}{x} ≥ 25

Esercizio n° 8

Risolvi la seguente disequazione numerica fratta.

\frac{5x}{11} – \frac{3}{22} > \frac{15x ^{2}-18}{33x}

Esercizio n° 9

Risolvi la seguente disequazione numerica fratta.

\frac{1}{5} x – \frac{1}{x - 5}  > \frac{x + 1}{5}  – \frac{x - 1}{x - 5}

Esercizio n° 10

Risolvi la seguente disequazione numerica fratta.

x – \frac{1}{2 - 3x}  > \frac{2x - 1}{2}  + \frac{6x+1}{3x -2}

Esercizio n° 11

Risolvi la seguente disequazione letterale fratta.

\frac{2a}{x - a} + \frac{3}{4} ≤ 0

Esercizio n° 12

Risolvi la seguente disequazione letterale fratta.

\frac{10 + 7a}{x - a} + \frac{5(2 + x)}{a - x} < 3

 

Svolgimento

Esercizio n° 1

Risolvi la seguente disequazione numerica fratta.

\frac{2x + 3}{4x + 4} – 1 ≤ \frac{x - 1}{x + 1}

\frac{2x + 3}{4(x + 1)}  – 1 ≤ \frac{x - 1}{x + 1}

Si riporta tutto al primo membro

\frac{2x + 3}{4(x + 1)}  – 1 –  \frac{x - 1}{x + 1} ≤ 0

\frac{2x + 3-4(x +1)-4(x - 1)}{4(x + 1)}   ≤ 0   C.E.   x + 1 ≠ 0 ⇒  x ≠ – 1

\frac{2x + 3-4x -4-4x +4}{4(x + 1)}   ≤ 0   ⇒   \frac{-6x + 3 }{4(x + 1)}  ≤ 0

A questo punto si deve studiare il segno della frazione, si studia separatamente il numeratore e il denominatore ponendoli maggiori di zero.

N > 0   ⇔ – 6x + 3 ≥ 0 ⇒  -6x >  – 3  ⇒  6x < 3  ⇒  x < \frac{3 }{6}   semplificando  x < \frac{1 }{2}

D > 0 ⇔ 4(x + 1) > 0 ⇒ 4x + 4 > 0 ⇒   4x > -4 ⇒  x > -1  il denominatore solo maggiore perchè il risultato annulla la disequazione

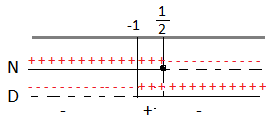
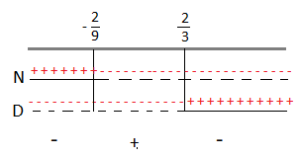
Riportiamo i risultati sulle rette.

 

A questo punto consideriamo la disequazione di partenza che è negativa, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli negativi che sono:   x < – 1  e x ≥ \frac{1 }{2}

Esercizio n° 2

Risolvi la seguente disequazione numerica fratta.

\frac{1}{x } < 0     C.E. x ≠0

x > 0

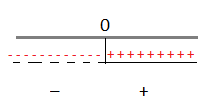
disequazione-2

Riportiamo i risultati sulle rette.

A questo punto consideriamo la disequazione di partenza che è negativa, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli negativi che corrispondono a x < 0

Esercizio n°3

Risolvi la seguente disequazione numerica fratta.

\frac{1}{x-1 } > 0     C.E.  x – 1 ≠ 0 ⇒  x ≠ 1

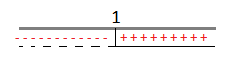
x – 1 > 0 ⇒  x > 1

disequazione-3

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono a x > 1

Esercizio n° 4

Risolvi la seguente disequazione numerica fratta.

\frac{x+1}{x} > 0   C.E.   x ≠ 0

N: x + 1 > o  ⇒ x > – 1

D: x > 0

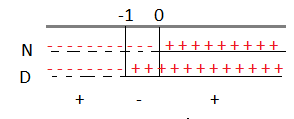
Riportiamo i risultati sulle rette.

disequazione-4

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono a x < – 1 e x > 1.

Esercizio n° 5

Risolvi la seguente disequazione numerica fratta.

\frac{1 - x}{2x} ≥ 0     C.-E.   2x ≠ 0 ⇒ x ≠ 0

N: 1 – x  ≥ 0  ⇒  -x ≥ – 1 ⇒  x ≤ 1

D: 2x > 0  ⇒ x > 0

Riportiamo i risultati sulle rette.

disequazione-5

 

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono  0<x ≤ 1

Esercizio n° 6

Risolvi la seguente disequazione numerica fratta.

\frac{3x - 6}{2x + 1} ≥ 0    C.E  2x + 1 ≠ 0 ⇒  x ≠ – \frac{1 }{2}

N: 3x – 6 ≥ 0 ⇒  3x ≥ 6 ⇒  x ≥ 2

D: 2x + 1 > 0 ⇒ 2x > -1   ⇒ x  > – \frac{1 }{2}

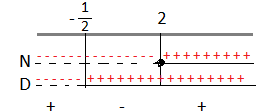
Riportiamo i risultati sulle rette.

disequazione-6

 

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono  x < \frac{1 }{2}  e  x ≥ 2

Esercizio n° 7

Risolvi la seguente disequazione numerica fratta.

\frac{5}{x} ≥ 25      C.E. x ≠ 0

\frac{5}{x} – 25  ≥ 0  ⇒  \frac{5 - 25x }{x}    ≥ 0

N : 5 – 25x ≥ 0  ⇒  -25x ≥  – 5  ⇒  25x ≤ 5   ⇒  x ≤ \frac{1}{5}

D : x > 0

Riportiamo i risultati sulle rette.

disequazione-7

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: 0 < x ≤ \frac{1}{5}

Esercizio n° 8

Risolvi la seguente disequazione numerica fratta.

\frac{5x}{11} – \frac{3}{22} > \frac{15x ^{2}-18}{33x}

\frac{5x}{11} – \frac{3}{22} – \frac{15x ^{2}-18}{33x}  > 0

\frac{30x^{2}-9x-30x^{2}+36}{66x} > 0     C.E.   66x ≠ 0⇒ x≠ 0

N: 30x² – 9x – 30x² + 36> 0   ⇒ -9x > -36  ⇒   9x< 36  ⇒ x < 4

D: 66x > 0  ⇒   x> 0

Riportiamo i risultati sulle rette.

disequazione-8

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: 0 < x < 4

Esercizio n° 9

Risolvi la seguente disequazione numerica fratta.

\frac{1}{5} x – \frac{1}{x - 5}  > \frac{x + 1}{5}  – \frac{x - 1}{x - 5}

\frac{1}{5} x – \frac{1}{x - 5}  – \frac{x + 1}{5}  + \frac{x - 1}{x - 5}  > 0

\frac{x(x - 5)-5-(x-5)(x + 1)+5(x-1)}{5(x-5)} > 0   C.E.  x – 5 ≠ 0 ⇒  x ≠ 5

N: x² – 5x – 5- (x² + x – 5x – 5 ) + 5x – 5 > 0  ⇒  x² – 5x – 5 –x² – x + 5x + 5 + 5x – 5 > 0⇒  -x +5x- 5> 0  ⇒4x >5 ⇒x>\frac{5}{4}

D: 5 (x – 5) > 0  ⇒  x  > 5

Riportiamo i risultati sulle rette.

disequazione-9

 

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: x < \frac{5}{4} e x > 5

Esercizio n° 10

Risolvi la seguente disequazione numerica fratta.

x – \frac{1}{2 - 3x}  > \frac{2x - 1}{2}  + \frac{6x+1}{3x -2}

x – \frac{1}{2 - 3x}   –  \frac{2x - 1}{2}  – \frac{6x+1}{3x -2}  > 0

x + \frac{1}{3x - 2}  –  \frac{2x - 1}{2}  – \frac{6x+1}{3x -2}  >  0

\frac{2x(3x - 2)+2-(2x -1)(3x - 2) -2(6x + 1)}{2(3x - 2)} >  0    C.E. 3x – 2 ≠ 0 ⇒  x ≠ \frac{2}{3}

N: 6x² -4x + 2 – (6x² – 4x – 3x + 2) – 12x – 2 >  0 ⇒  6x² –4x + 2 – 6x² +4x + 3x – 2 – 12x – 2  >  0 ⇒ -9x – 2  >  0 ⇒ 9x+2<0  ⇒  x < – \frac{2}{9}

D: 2(3x – 2) >  0 ⇒  x >\frac{2}{3}

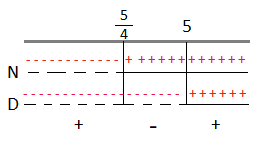
Riportiamo i risultati sulle rette.

disequazione-10

A questo punto consideriamo la disequazione di partenza che è positiva, quindi dovremo prendere dal grafico come soluzioni solo gli intervalli positivi che corrispondono: – \frac{2}{9}< x < \frac{2}{3}

Esercizio n° 11

Risolvi la seguente disequazione letterale fratta.

\frac{2a}{x - a} + \frac{3}{4} ≤ 0    C.E   x – a ≠0

\frac{8a + 3(x - a)}{4(x-a)} ≤ 0

\frac{8a + 3x - 3a}{4(x-a)} ≤ 0

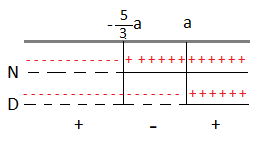
\frac{5a + 3x }{4(x-a)}  ≤ 0

N: 5a + 3x ≥ 0 ⇒ 3x ≥ -5a ⇒  x ≥ -\frac{5}{3}a

D: 4(x – a) > 0 ⇒ x  > a

Adesso poichè il parametro a è presente solo nel termine noto abbiamo proceduto in maniera normale senza fare alcuna discussione.

Le soluzioni saranno quelle negative e uguali ai numeri

Esercizio n° 12

Risolvi la seguente disequazione letterale fratta.

\frac{10 + 7a}{x - a} + \frac{5(2 + x)}{a - x} < 3

\frac{10 + 7a}{x - a} – \frac{5(2 + x)}{x - a}  – 3 <0    C.E. x-a≠0 ⇒ x ≠ a

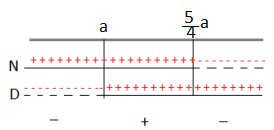
\frac{10 + 7a-5(2+x)-3(x-a)}{x - a}  <0

N: 10 + 7a – 10 – 5x -3x +3a  >0 ⇒ 10a -8x >0  ⇒ 8x – 10a < 0  ⇒ x < \frac{10}{8}a ⇒ x < \frac{5}{4} a

D: x – a >0⇒ x >a

Adesso poichè il parametro a è presente solo nel termine noto abbiamo proceduto in maniera normale senza fare alcuna discussione.

Le soluzioni saranno quelle negative

 

Programma di matematica secondo superiore

 

 

ImpariamoInsieme