MEDIANE DI UN TRIANGOLO E BARICENTRO
mediana e baricentroDisegniamo un triangolo acutangolo, rettangolo e ottusangolo e notiamo che le tre mediane s’incontrano nel punto K . Questo punto detto baricentro, è sempre interno al triangolo.
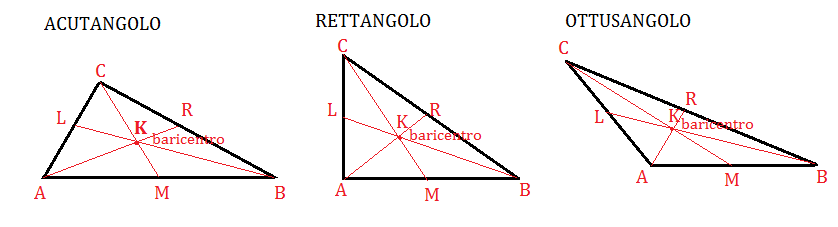
Consideriamo ancora le tre mediane e osserviamo che il baricentro divide ciascuna di esse in due parti; per esempio la mediana CM è divisa da K in CK e KM . Se misuriamo questi due segmenti ci accorgiamo che sono uno il doppio dell’altro: CK= 2 KM e lo stesso per le altre mediane: AK = 2 KR e BK= 2KL.
Diciamo che il baricentro divide ogni mediana in due parti tali che quello che contiene il vertice è doppia dell’altra.
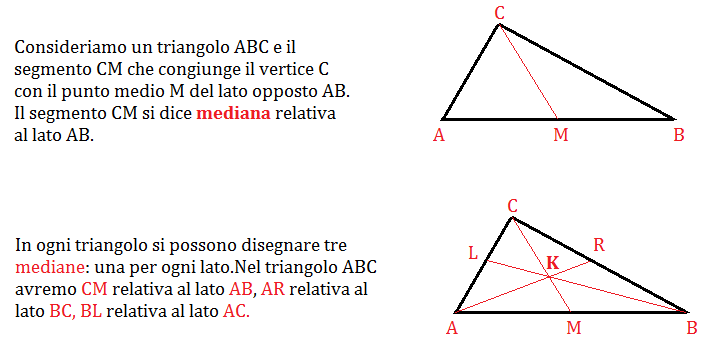
Possiamo dire che: la mediana di un triangolo relativa ad un lato è il segmento che unisce il punto medio del lato con il vertice opposto.
Le tre mediane si incontrano in un unico punto detto baricentro, che è sempre interno al triangolo.
In un triangolo rettangolo la mediana relativa all’ipotenusa è metà dell’ipotenusa stessa.