La rotazione è un’isometria che studieremo in questo articolo.
La rotazione è un’isometria.
Fissiamo un punto O nel piano π e consideriamo un angolo α; fissiamo anche un verso dove ruotare, per esempio in senso antiorario ↶ . Al punto P є π facciamo corrispondere il punto P’є π tale che l’angolo POP’ sia congruente ad α e OP’ sia congruente a OP. Il punto P subisce, cosi, una rotazione di ampiezza α ( di raggio OP) fino ad assumere la posizione di P’.
Si è così ruotata la figura nel piano. Il punto O è detto centro della rotazione ed α angolo di rotazione, il punto P’ si dice corrispondente di A nella rotazione R. Si ha, pertanto, la seguente definizione:
La rotazione è un movimento diretto individuato da un punto fisso O, detto centro, e da un angolo orientato che ne stabilisce l’ampiezza e il verso di spostamento nel piano.
Essa, di solito, viene indicata col simbolo R(O,α) , dove O è il centro ed α l’angolo. Ovviamente, viene fissato anche il verso : in senso antiorario oppure orario.
A) Proprietà invarianti della rotazione.
Essa:
1. Conserva le distanze.
2. Trasforma retta in retta.
3. Conserva il parallelismo. Cioè, a rette parallele fa corrispondere rette parallele.
4. Conserva la perpendicolarità. Cioè, a rette perpendicolari fa corrispondere rette perpendicolari.
5. Conserva l’ampiezza degli angoli.
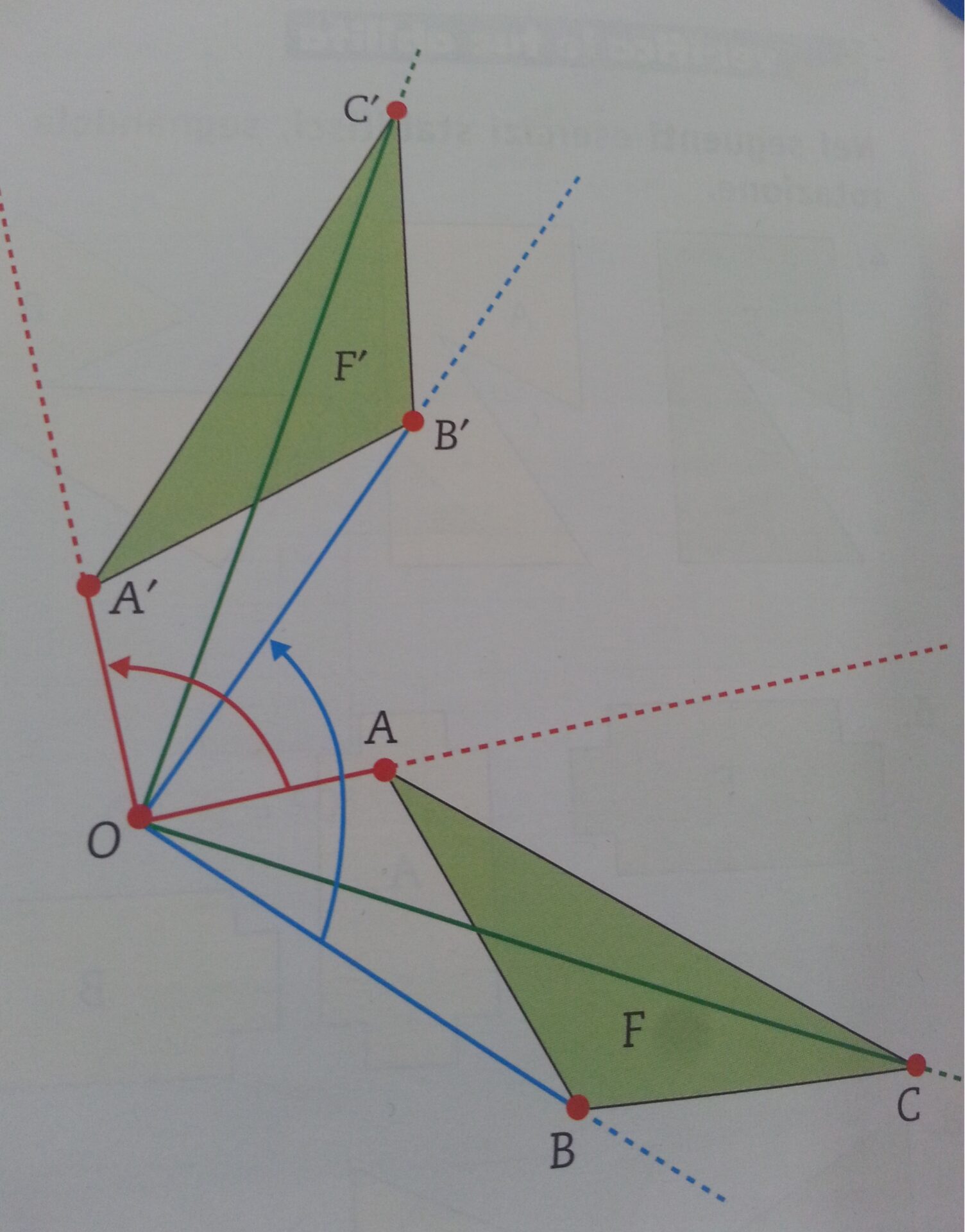
Data la rotazione R, individuata dal centro O e dell’angolo α di ampiezza 90°, per disegnare la figura F’, corrispondente di una figura F assegnata secondo la rotazione R, basterà disegnare i vertici A’, B’, C’, corrispondenti dei vertici A, B e C.
Se sovrapponiamo il triangolo ABC al triangolo A’B’C’, vedremo che le due figure coincidono in ogni punto e, poichè per sovrapporli non usciamo dal piano in cui giacciono, diciamo che le due figure sono direttamente congruenti.
Quindi:due figure che si corrispondono in una rotazione sono direttamente congruenti.