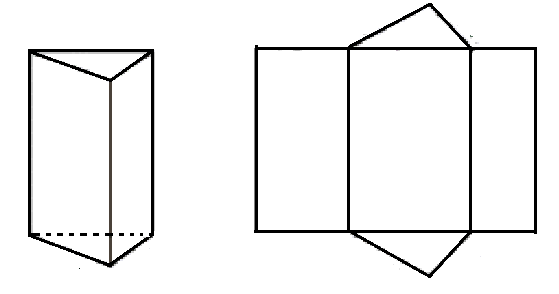
Prendiamo il modello di un prisma retto avente per basi due triangoli, costruito con un cartoncino.
Tagliamolo lungo uno spigolo laterale e lungo tutti gli spigoli di base, eccetto uno e stendiamolo su un piano.
Questa figura piana detta sviluppo della superficie totale del prisma ed è costituita da due poligoni congruenti ( le basi del prisma) e da un rettangolo avente la base lunga come il perimetro di una base del prisma e l’altezza lunga come l’altezza del prisma.
Tale rettangolo è lo sviluppo della superficie laterale del prisma.
La regola quindi è:
La misura dell’area della superficie laterale di un prisma retto si ottiene moltiplicando la misura della lunghezza del perimetro di una base per la misura della lunghezza dell’altezza del prisma.
Indicando con A(l) l’area della superficie laterale, con 2p il perimetro di ciascuna delle due basi del prisma, con h la misura dell’altezza del prisma otteniamo la formula:
A(l) = 2p · h
Dalla formula diretta si possono ricavare le formule inverse per calcolare l’altezza e il perimetro di base:
e
La misura dell’area della superficie totale di un prisma retto si ottiene addizionando alla misura dell’area della superficie laterale la misura dell’area delle due basi.
Da questa possiamo ricavare le formule inverse che ci permettono di calcolare l’area della superficie laterale e l’area di base:
e