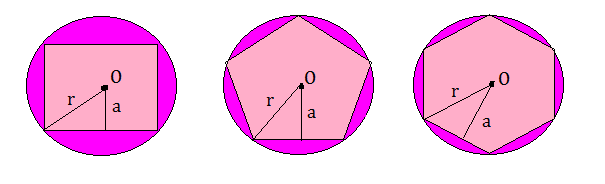
Consideriamo alcune circonferenze aventi tutti il raggio di uguale lunghezza e in ciascuno di essi è inscritto un poligono regolare.
Dall’osservazione della figura rileviamo che l’area della parte di piano limitata dalla circonferenza e dal contorno del poligono diminuisce se si aumenta il numero dei lati del poligono regolare inscritto.
Quindi, se consideriamo un poligono regolare inscritto con un numero molto grande di lati, possiamo intuitivamente affermare che il contorno del poligono si avvicina sempre di più alla circonferenza cioè tende a confondersi con la circonferenza stessa, e l’apotema tende a confondersi con il raggio della circonferenza. Ne deduciamo che un cerchio può essere considerato come un poligono regolare con un numero grandissimo di lati: il contorno di questo poligono è la circonferenza e il suo apotema è il raggio. Quindi la misura dell’area del cerchio si può calcolare usando la formula:
possiamo scrivere che l’area del cerchio :
poichè C= 2π · r si ottiene:
da cui si ricava la formula inversa che permette di trovare la lunghezza del raggio data l’area del cerchio:
L’area di un cerchio si ottiene moltiplicando il quadrato della misura del raggio per π.
Per calcolare il valore dell’area del cerchio approssimato a meno di 1\100 si usa π= 3,14