Consideriamo un triangolo rettangolo ABC e facciamolo ruotare di un giro completo (360°) intorno alla retta a (asse di rotazione) passante per un suo cateto per esempio AC. Otteniamo un solido detto cono.
Esso è il solido ottenuto dalla rotazione completa di un triangolo rettangolo intorno all’asse che è la retta passante per uno dei suoi cateti.
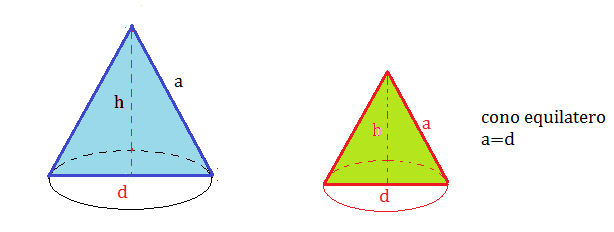
Se tagliamo un cono con un piano passante per l’asse otteniamo una sezione: un triangolo isoscele che ha per base il diametro della base del cono e per altezza la sua altezza e per lato obliquo l’apotema della figura conica
Se tale sezione è un triangolo equilatero, allora l’apotema è congruente con il diametro di base ed esso è detto equilatero.
Il raggio di base r e l’altezza h sono i cateti di un triangolo rettangolo in cui l’apotema rappresenta l’ipotenusa e quindi è possibile applicare il teorema di Pitagora: