Equazioni di secondo grado
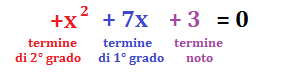
Le equazioni di secondo grado sono quelle in cui il grado massimo dei suoi termini è 2.
Tali equazioni non sono di facile soluzione. In questo corso di studio si considerano solo le equazioni pure cioè quelle in cui è presente solo il termine noto e il termine di 2° grado.
Per esempio: x² – 25 = o è un’equazione pura
Un’equazione di 2° grado si dice pura se non contiene termini di 1° grado.
Per risolvere un’equazione di secondo grado si eseguono una serie di passaggi che portano a un’equazione nella forma normale equivalente a quella data, per esempio:
– 5x + x(4x + 3) = – 2x + 49 si eliminano le parentesi
-5x + 4x² + 3x = -2x + 49 si applica la regola del trasporto
– 5x + 4x² + 3x + 2x = + 49 si riducono i termini simili
+ 4x² = + 49 equazione in forma normale
Si applica il 2° principio di equivalenza:
da cui
Si estrae la radice quadrata:
quindi:
e
Questo perchè sia il quadrato di un numero positivo , sia il quadrato di un numero negativo
sono uguali a
.
L’equazione ha quindi due soluzioni date da numeri relativi opposti.
Se abbiamo x² = – 9 essa non ha soluzioni perchè non è un numero reale.
In generale, un’equazione pura di 2° grado si può scrivere in forma normale:
ax² = b con a≠ 0 la formula risolutiva è:
quindi:
- se b\a > 0 l’equazione ammette due soluzioni opposte
e
- se b\a <0 l’equazione si dice impossibile cioè non ammette soluzioni in quanto nell’insieme R non esiste la radice quadrata di un numero negativo.