Frazioni
Per rappresentare in simboli una frazione si scrivono due numeri naturali separati da un tratto orizzontale detto linea di frazione.
Il numero scritto sotto la linea di frazione si dice denominatore e indica in quante parti uguali si deve dividere la grandezza considerata.
Il numero scritto sopra la linea di frazione si dice numeratore e indica quante di tali parti si devono considerare.
Il numeratore e il denominatore si dicono termini della frazione:
m\n →linea di frazione m=numeratore n=denominatore
Esempio

Per rappresentare una frazione si può prendere qualsiasi figura come una torta, una pizza, un quadrato…. importante è dividerlo in parti uguali, quindi tante parti quante indicate dal denominatore.
Ogni parte uguale in cui viene diviso l’intero si chiama unità frazionaria.
Due frazioni che insieme formano l’intero si dicono complementari.
Quindi due frazioni si dicono complementari se la loro somma è 1.
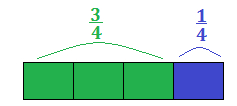
Per individuare una frazione m\n di un intero occorre dividere l’intero per il denominatore n e moltiplicare il risultato per il numeratore m
Esempio: abbiamo un segmento intero lungo 60 cm e dobbiamo calcolare i suoi 3\5
se facciamo (60:5)=12 → corrisponde ad 1\5 del segmento cioè l’unità frazionaria
se facciamo (12×3)=36 corrisponde ai 3\5 del segmento

Frazioni decimali
Le frazioni con denominatore uguale a 10, 100, 1000 si dicono frazioni decimali. Quindi la parte intera è stata divisa rispettivamente in 10, 100, 1000 parti.
L’ unità frazionaria 1\10 si legge un decimo.
Le quantità indicate dalle frazioni decimali si possono scrivere anche sotto forma di numeri con la virgola chiamati numeri decimali.
Confrontiamo le frazioni
- Quando due frazioni hanno lo stesso denominatore , è maggiore quella che ha il numeratore maggiore. Per esempio:
.
- Quando due frazioni hanno lo stesso numeratore, è maggiore quella che ha il denominatore minore. Per esempio:
.
Vedi frazioni proprie, improprie, e apparenti
Vedi gli esercizi
Programma matematica terza elementare
Programma matematica quarta elementare
Programma matematica quinta elementare