GRANDEZZE SCALARI E VETTORIALI
In fisica esistono due tipi di grandezze: scalari e vettoriali.
Le grandezze scalari per essere definite hanno bisogno solo di un numero e di una unità di misura. Esempi di questo tipo di grandezze è la temperatura, il tempo, la massa e l’energia.
Le grandezze vettoriale sono quelle che per essere completamente descritte devono essere accompagnate da altre informazioni oltre che al numero.
Infatti se per esempio diciamo che ci siamo allontanati 25 km in linea d’aria dal centro di Napoli, non diamo un’informazione esaustiva perchè possiamo aver raggiunti Castellamare di Stabia, Procida o tantissimi altri luoghi. Quindi per descrivere completamente il nostro spostamento dobbiamo specificare anche in quale direzione ci siamo mossi e lungo quale verso.
Quindi una grandezza vettoriale come lo spostamento è caratterizzata da:
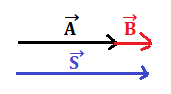
- un numero non negativo, detto modulo o intensità, che indica il suo valore rispetto all’unità di misura ed è la lunghezza della freccia;
- una direzione, che specifica l’orientamento ed è la retta su cui giace il vettore;
- un verso che è la punta della freccia.
Quindi in definitiva per definire lo spostamento dobbiamo avere la distanza tra il punto di partenza e d’arrivo, la direzione e cioè la retta che unisce i due punti e infine il verso lungo il quale viene percorsa la retta.
Per indicare una grandezza vettoriale si usa una freccia da porre sopra la lettera che indica il vettore, quindi: .
Per il vettore spostamento bisogna fare una considerazione, essendo esso la lunghezza della retta che congiunge il punto di partenza con quello di arrivo, cioè la distanza tra questi due punti; se per esempio si volesse calcolare lo spostamento lungo una pista di atletica di 400 m che ha la forma ovale allora il punto di partenza coinciderà con quello di arrivo quindi lo spostamento sarà nullo.
OPERAZIONI CON I VETTORI
ADDIZIONE DI VETTORE
I vettori si addizionano in modo diverso rispetto agli scalari, quindi la somma di due vettori non dipende solo dal loro modulo, ma anche dalla direzione e dal verso.
Quando si sommano due vettori e
con la stessa direzione e con lo stesso verso , il vettore somma
avrà lo stesso verso e la stessa direzione dei due vettori.
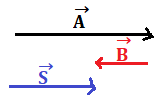
Se e
hanno la stessa direzione ma verso opposto e per esempio
ha modulo maggiore di
allora il vettore somma
avrà la direzione e il verso di
e il modulo uguale ad A-B.
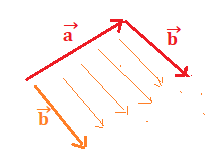
Pe sommare due vettori consecutivi e
ma che puntano in direzioni diverse è possibile applicare il metodo punta coda che avviene nel seguente modo: In presenza di due vettori non allineati si trasla il secondo vettore in modo che la punta del primo coincida con la coda dell’altro.
A questo punto si traccia il vettore somma che si ottiene congiungendo la coda di con la punta di
.
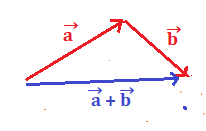
Per sommare vettori non paralleli, si può usare in modo equivalente al precedente il metodo del parallelogramma.
Per applicarlo se dobbiamo sommare due vettori e
, si sposta il vettore
senza ruotarlo e si fa in modo che la sua cosa coincida con quella di
, individuando così un parallelogramma.
Il vettore somma congiunge la coda di e di
con il vertice opposto del parallelogramma.
L’addizione di vettori gode delle seguenti proprietà:
- commutativa, dove
+
=
+
cioè la somma dei vettori è la stessa cambiando l’ordine degli addendi-
- associativa, dove (
+
) +
=
+ (
+
) cioè la somma di tre vettori si può calcolare addizionando a uno di essi la somma degli altri due e il risultato non dipende dall’ordine in cui vengono effettivamente addizionati.
LA MOLTIPLICAZIONE DI UN VETTORE PER UN NUMERO
Questa operazione non fa altro che modificare la lunghezza del vettore e nel caso il numero sia negativo ne cambia anche il verso.
Quindi = k •
dove il modulo sarà c=| k | • a cioè uguale al prodotto del valore assoluto di k per il modulo di
.
La direzione sarà la stessa di ;
Il verso è quello di se k è positivo, verso opposto se k è negativo.
Infatti moltiplicando il vettore per k= -1 otteniamo il vettore opposto di
che indicheremo con –
.
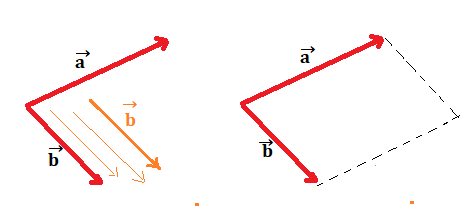
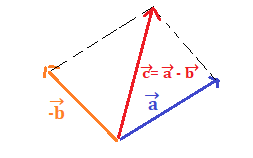
LA SOTTRAZIONE TRA DUE VETTORI
La differenza tra due vettori si ottiene sommando il primo di essi con l’opposto del secondo.
Per esempio se dovessimo fare la sottrazione tra e
. Abbiamo che
=
–
La prima cosa che si fa è disegnare il vettore – appunto l’opposto di
:
Poi si addiziona – ad
per esempio con il metodo del parallelogramma ma potremmo usare anche quello punta coda.
Il vettore =
–
quindi si ottiene addizionando ad
l’opposto di
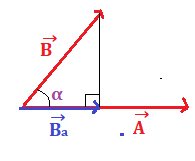
SENO E COSENO DI UN ANGOLO
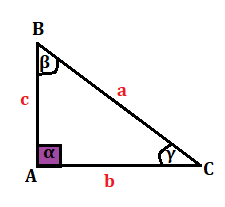
Prima d’introdurre il prodotto vettoriale e il prodotto scalare è bene spiegare una regola importante da applicare il un triangolo rettangolo ABC, con l’angolo retto nel vertice A.
Il seno per esempio di è uguale al rapporto del cateto opposto a
e l’ipotenusa.
il cateto opposto a è AB che abbiamo nominato c e l’ipotenusa BC abbiamo chiamato a. Quindi:
sen possiamo anche scriverlo come:
Il coseno di è uguale al rapporto del cateto adiacente a
e l’ipotenusa. Quindi:
Quindi generalizzando la regola possiamo dire:
- un cateto è uguale all’ipotenusa moltiplicata per il seno dell’angolo opposto al cateto;
- un cateto è uguale all’ipotenusa per il coseno dell’angolo adiacente al cateto.
Spesso nei problemi è possibile utilizzare anche la formula con la tangente dove . Molto utile nei problemi in cui il vettore è scomposto nelle sue componenti.
SCOMPOSIZIONE DI UN VETTORE LUNGO DUE DIREZIONI E LUNGO GLI ASSI CARTESIANI
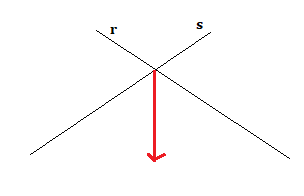
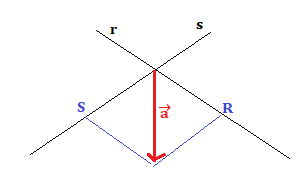
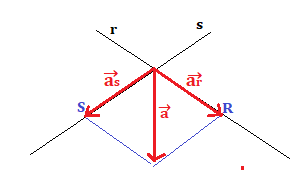
Consideriamo due rette incidenti r e s e un vettore posto sul piano delle due rette , chiameremo vettori componenti di
lungo r ed s i due vettori che chiameremo
e
che avranno come caratteristica quella di essere paralleli ad r e s e
+
=
Vediamo graficamente cosa succede. Prima di tutto facciamo in modo che la coda di coincida con il punto d’intersezione delle due rette.
A questo punto proiettiamo la punta di sulla retta r parallelamente ad s e sulla retta s parallelamente ad r, trovando i punti R ed S.
I due vettori componenti di congiungono la coda di
con i punti R e S.
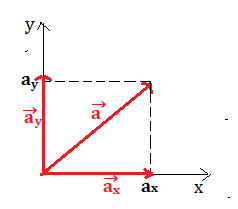
Se un vettore lo vogliamo scomporre lungo gli assi cartesiani , poniamo la coda del vettore nell’origine degli assi, accadrà che la sua punta avrà come coordinate che sono uguali ai moduli dei vettori
e
.
Se applichiamo il teorema di Pitagora a uno dei due triangoli rettangoli che si viene a formare, possiamo calcolare il vettore conoscendo le componenti, oppure si può calcolare anche una delle componenti conoscendo il vettore e l’altra componente.
Inoltre possiamo introdurre anche un particolare vettore chiamato versore che ha modulo 1. Quindi un vettore A scomposto nelle sue componenti cartesiane può essere scritto anche così:
Le componenti cartesiane, seguendo le regole di trigonometria scritte nel paragrafo precedente, possono essere calcolate come:
OPERAZIONI CON I VETTORI IN COMPONENTI CARTESIANE
Dati due vettori : e
vediamo le varie operazioni con le coordinate cartesiane:
la somma: in componenti
e
la differenza: in componenti
e
la moltiplicazione di un vettore per un numero, per esempio per un numero k è uguale si otterrà un vettore
in questo modo:
e
IL PRODOTTO SCALARE DI DUE VETTORI
Partiamo dalla definizione:
Il prodotto scalare di due vettori è lo scalare uguale al prodotto del modulo del primo vettore per la proiezione del secondo vettore sul primo quindi:
Tale prodotto sarà positivo se il vettore e la proiezione hanno lo stesso verso.
Negativo se hanno verso opposto
Nullo se i due vettori sono perpendicolari tra loro
Per calcolare il prodotto scalare ovviamente si può indifferentemente utilizzare la proiezione di su
o viceversa.
Se utilizziamo le regole della trigonometria possiamo scrivere il prodotto scalare in modo diverso quindi:
Vediamo graficamente perchè è possibile ciò:
Se utilizziamo la proiezione di su
allora avremo :
In generale il prodotto vettoriale si potrà scrivere in questo modo:
dove α è l’angolo compreso tra i due vettori.
Il prodotto scalare gode delle seguenti proprietà:
- commutativa, quindi il prodotto scalare non cambia cambiando l’ordine degli addendi :
- distributiva rispetto all’addizione, quindi: (
+
) •
=
•
+
•
.
Il prodotto scalare si può calcolare anche a partire dalle componenti cartesiane dei vettori e
Quindi il prodotto scalare dei vettori e
è
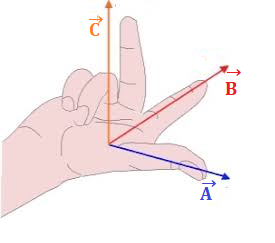
PRODOTTO VETTORIALE DI DUE VETTORI
Il prodotto vettoriale di due vettori e
è il vettore
=
×
che ha:
- modulo uguale all’area del parallelogramma che ha per lati i due vettori;
- direzione perpendicolare al piano che contiene i vettori;
- verso che si ottiene con la regola della mano destra, cioè il verso uscente dal palmo della mano destra se il pollice è posto nel verso di
e le altre dita nel verso di
.
Quindi ricordando la definizione di seno :
Possiamo riscrivere l’area del parallelogramma diversamente:
ovviamente se consideriamo avremo la stessa formula.
Quindi i definitiva possiamo scrivere che il modulo del prodotto vettoriale è uguale:
dove l’angolo α è quello compreso tra i due vettori.
Le proprietà del prodotto vettoriale sono le seguenti:
- anticommutativa, cioè il prodotto vettoriale cambia il verso se cambia l’ordine dei vettori, quindi:
- distributiva rispetto all’addizione:
e