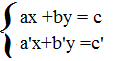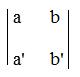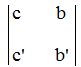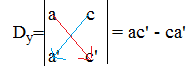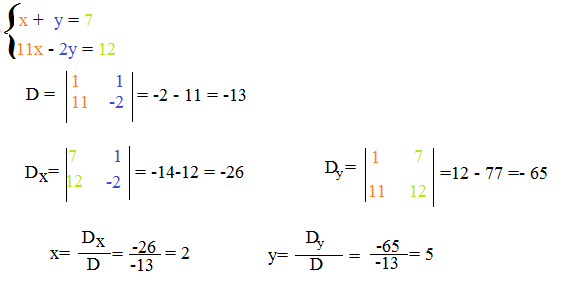Il metodo di Cramer come gli altri metodi il sistema deve essere ridotto in forma normale prima di poter svolgere l’esercizio.
Quindi deve essere scritto in questo modo:
Per poter usare questo metodo dobbiamo conoscere dei termini e cioè quella di determinante.
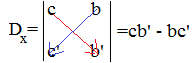
Chiamiamo determinante del sistema il numero D che si ottiene nel seguente modo:
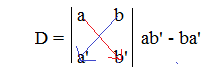
Nella prima colonna si mettono i coefficienti delle x delle due equazioni e nella seconda quelli delle y. La D è il valore del determinante dei coefficienti che si ottiene moltiplicando in croce nello schema , partendo dal primo numero in alti a sinistra e sottraendo i numeri ottenuti:
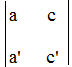
Poi bisogna calcolare il determinante dell’incognita x .
Questo schema nella prima colonna ha i termini noti delle due equazioni del sistema e e nella seconda colonna i coefficienti delle y. Il determinante dell’incognita x è il numero che si ottiene moltiplicando in croce nello schema come per il determinante precedente.
Infine bisogna calcolare il determinante dell’incognita y.
Nella prima colonna vanno i coefficienti dell’incognita x delle due equazioni del sistema e nella seconda colonna i termini noti. Il valore del determinante è il numero che si ottiene moltiplicando in croce nello schema.
Utilizzando il determinante dei coefficienti e i determinanti delle due incognite, si possono risolvere tutti i sistemi lineari.
Se D è diverso da zero il sistema è determinato e la soluzione è:
Se D=0 e = 0 oppure
=0 il sistema è indeterminato
Se D=0 e ≠ 0 oppure
≠0 il sistema è impossibile
ESEMPI
1° esempio
2° esempio
A questo punto poichè il discriminante è 0 e quindi si deve vedere il oppure il
com’è. se anch’esso è uguale a 0 allora il sistema è indeterminato, se invece è diverso da zero allora è impossibile. In questo caso quindi è impossibile.