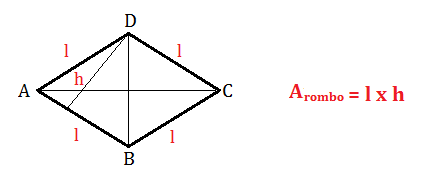
L’AREA DEL ROMBO
Il rombo è un parallelogramma con i lati congruenti tra loro. Se sono note le misure di un suo lato (l) e dell’altezza (h) a esso relativa, la sua area si calcola con la formula vista per il parallelogramma:
Se conosciamo la misura delle diagonali, possiamo calcolare l’area in un altro modo:
Un rombo è equivalente alla metà di un rettangolo che ha per lati le diagonali del rombo.
L’area del rombo è uguale al semiprodotto della lunghezza delle sue diagonali.
formula diretta dove
indicano le misure delle sue diagonali.
Le formule inverse sono:
ci permette di calcolare la diagonale maggiore conoscendo l’area e la diagonale minore;
ci permette di calcolare la diagonale minore conoscendo l’area e la diagonale maggiore;
Poichè il quadrato è un particolare rombo con le diagonali congruenti, allora l’area del quadrato si può calcolare anche così:
formula diretta dove d indica la misura della diagonale.
formula inversa che ci permette di calcolare la diagonale conoscendo l’area.
Anche l’area di un quadrilatero con le diagonali perpendicolari si calcolerà come l’area del rombo.