Tutti i numeri razionali assoluti formano un nuovo insieme che si indica con . Nell’insieme
è sempre possibile eseguire la divisione, che quindi è un’operazione interna a
.
L’insieme è un ampliamento dell’insieme N, ovvero l’insieme
contiene l’insieme N: N⊂
.
Quindi l’insieme N è un sottoinsieme dell’insieme .
Quindi ogni numero naturale si può scrivere sotto forma di numero razionale assoluto.
- Ogni frazione con il numeratore uguale a 0 è uguale al numero naturale 0, ovvero il numero 0 si può sempre scrivere sotto forma di frazione con numeratore uguale a 0:
0\1= 0:1 = 0 ; 0\10= 0:10= 0 ; 0\105 = 0:105= 0…..
- Ogni frazione apparente con il numeratore uguale al denominatore è uguale a 1; ovvero il numero 1 si può sempre scrivere sotto forma di frazione con numeratore e denominatore uguali:
5\5 = 5:5 = 1; 22\22 = 22:22 = 1; 35\35 0 35:35 = 1
- Ogni frazione con il denominatore uguale a 1 o con il numeratore multiplo del denominatore è uguale a un numero naturale, ovvero ogni numero naturale si può sempre scrivere sotto forma di frazione con denominatore uguale a 1 o numeratore multiplo del denominatore:
5\1 = 5:1 = 5; 10\5 = 10:5 = 2; 45\9= 45:9 = 5
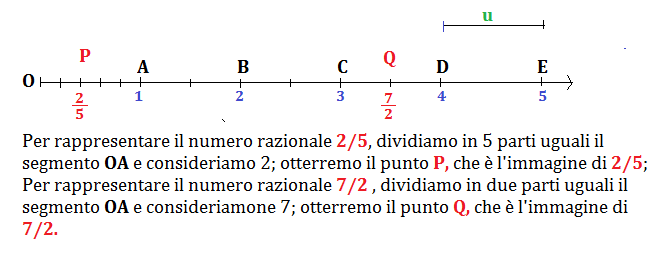
Anche i numeri razionali , come i numeri naturali, possono essere rappresentati su una retta orientata.