APPLICAZIONE DEL TEOREMA DI PITAGORA AL TRAPEZIO RETTANGOLO
Il teorema di Pitagora come ben sappiamo si può applicare a tutte quella figure geometriche dalle quali si può ricavare un triangolo rettangolo. Quindi lo possiamo applicare al rombo, al quadrato, al rettangolo, al triangolo isoscele ecc. perchè la lista si potrebbe prolungare anche alle figure solide.
;
;
ESEMPIO
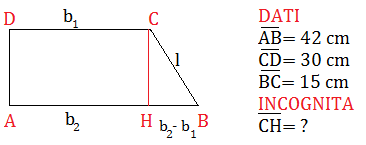
Calcola la misura dell’altezza di un trapezio rettangolo che ha le basi lunghe 42 cm e 30 cm e il lato obliquo di 15 cm.
SVOLGIMENTO
HB= AB-CD= (42-30) cm =12 cm
Applichiamo il teorema di Pitagora al triangolo rettangolo CHB per calcolare CH: