Esercizio
Svolgi le seguenti disequazioni di secondo grado.
1)
2)
3)
4)
5)
6)
7)
8)
9)
SVOLGIMENTO
Esercizio
Svolgi le seguenti disequazioni di secondo grado.
1)
La prima cosa da fare è porre numeratore e denominatore maggiore di zero.
N: 9x² + 2 >0 ⇒ x² >- 2\9 ma un numero al quadrato è sempre maggiore di un numero negativo quindi la soluzione è per ogni x appartenente a R.
D: x² – 5x + 6 >0 vado a considerare l’equazione associata:
x² – 5x + 6 =0 e mi vado a calcolare le radici.
Δ= b²-4ac= 25 – 24 = 1
Δ>0 , disequazione >0, allora le soluzioni saranno esterne: x<2 e x>3
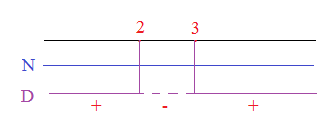
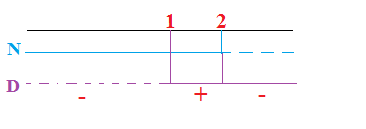
Portiamo ora le soluzioni del numeratore e del denominatore sul grafico, facendo attenzione a prendere le soluzioni negative visto che la disequazione fratta di partenza era <0
La soluzione è : 2<x<3
2) C.E. 2x-3≠0 quindi x ≠3\2
Poniamo numeratore e denominatore maggiore di zero.
N: x² + 4x -5 > 0
Δ= b²-4ac= 16 + 20 = 36
Δ>0 , disequazione >0, allora le soluzioni saranno esterne: x<-5 e x >1
D: 2x – 3 > 0⇒ x >3\2
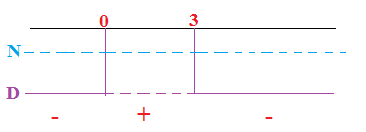
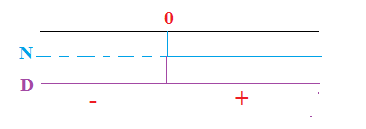
Riportiamo le radici trovate per il numeratore e il denominatore prendendo le soluzioni negative visto che la disequazione fratta è minore di zero.
La soluzione è : x<-5 e 1<x<3\2
3)
Poniamo numeratore e denominatore maggiore di zero.
N: -x² + 2x -4 > 0 ⇒ x² – 2x +4< 0
Δ= b²-4ac= 4 -16 = – 12<0
Δ<0 disequazione <0 allora non esiste x appartenente ad R.
D:x²+8 >0 quindi x²> -8 in questo caso un numero positivo come il quadrato deve essere per forza maggiore di un numero negativo, quindi il risultato è per ogni x ∈R.
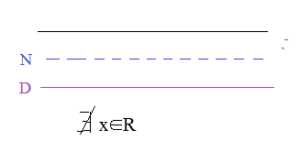
In questo caso la disequazione fratta non ha soluzioni perchè se andiamo a porre le radici del numeratore e del denominatore sul grafico, notiamo che non c’è mai una zona positiva, infatti:
4)
A questo punto poniamo numeratore e denominatore maggiore e uguale a zero.
N: 25x² -4 ≥0 considero l’equazione associata.
25x² -4 =0
Poichè il delta è maggiore di zero è la disequazione è maggiore di zero le soluzioni saranno esterne quindi:
e
D: 5(5x -1) >0 ⇒ x ≥ 1\5
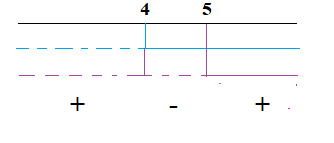
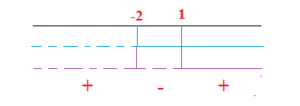
Riportiamo le radici trovate sul grafico.
Poichè la disequazione iniziale è ≤0, prenderemo le soluzioni negative e cioè: x< -2\5 e 1\5<x≤2\5
Al 4 non è anche uguale per la condizione di esistenza.il denominatore deve esser diverso da 1\5
5)
facciamo il m.c.m. che è x(x-3)
andiamo a porre numeratore e denominatore maggiore di zero
N: -x² -2 > 0 ⇒ x² + 2 < 0
x² <-2 impossibile
D: x(x-3) > 0
abbiamo x > 0 e x-3> 0 quindi x > 0 e x>3 in questo caso il Δ è >0, la disequazione> 0, allora le soluzioni sono esterne e cioè: x<0 e x>3.
Portiamo le soluzioni del numeratore e del denominatore sul grafico e otteniamo:
La disequazione fratta iniziale è negativa quindi prenderemo i risultati negativi: x<0 e x>3.
6)
N: 21x-45>0 Quindi :
D: 2x²(x-3)²> 0
2x²> 0e (x-3)² >0 quindi
2x²> 0 x≠0
(x-3)² >0 x≠ 3
Riporto i risultati del numeratore e del denominatore sul grafico:
Poichè le soluzioni da considerare sono positive la soluzione è:
con x≠ 3
7)
Poniamo numeratore e denominatore maggiore di zero:
N: x-5> 0 ⇒ x > 5
x-4 > 0 ⇒ x> 4
Portiamoli sul grafico:
Le soluzioni sono positive e cioè: x<4 e x>5. Dopo le metteremo sul grafico con le soluzioni del denominatore.
D: 2-x > 0 e x -1 > 0
x-2 < 0 ⇒ x < 2
x> 1
Riporto i risultati del numeratore e del denominatore sul grafico:
La disequazione è maggiore di zero, prenderemo i risultati positivi, quindi: 1 <x<2
A questo punto mettiamo entrambe i risultati sul grafico: quindi x<4 e x>5 e 1 <x<2
La soluzione è 1 <x<2 e 4 <x<5
8)
Poniamo numeratore e denominatore maggiore di zero.
N: 10x> 0 ⇒ x> 0
D: 2(x+2)²> 0 per ogni x ∈ R perchè un quadrato è sempre maggiore di zero.
Riportiamo i valori trovati su un grafico e otteniamo:
Poichè la disequazione fratta iniziale è minore di zero, prenderemo i risultati negativi, quindi: x<0.
9) C.E. : x+2 ≠0 e x-1≠0 quindi x ≠-2 e x≠ 1
Poniamo numeratore e denominatore maggiore di zero.
N: 3x² – 15x ≥ 0 ⇒ 3x(x – 5) ≥ 0 quindi considerando l’equazione associata otteniamo x=0 e x =5. Possiamo metterli sul grafico, oppure se consideriamo che il delta è maggiore di zero e la disequazione è maggiore di zero allora le soluzioni sono esterne. Quindi: x≤0 e x≥ 0
D: 3(x -1)(x +2)> 0 abbiamo che x>1 e x >-2 tali valori li portiamo sul grafico per capire quali sono le soluzioni del denominatore.
Le soluzioni sono x<-2 e x>1.
A questo punto possiamo mettere le soluzioni di numeratore e denominatore sul grafico finale e otteniamo:
Poichè la disequazione fratta iniziale è minore di zero, prenderemo i risultati negativi, quindi: -2<x≤0 e 1<x≤5