Le disequazioni fratte contengono l’incognita anche al denominatore, ridotte in forma normale si presentano nella seguente forma:
 e
e  .
.
A(x) e B(x) sono polinomi nella variabile x, anche se il numeratore potrebbe essere anche solo una costante.
Il procedimento per calcolarle prevede lo studio del segno della frazione. Si studia il segno del numeratore e del denominatore indipendentemente dal verso dell’equazione, quindi si pongono entrambe maggiore di zero. Solo dopo aver trovato le soluzioni del numeratore e del denominatore e a seconda del verso della disequazione, si troveranno i risultati della disequazione frazionaria.
Se la frazione è > 0 si prenderanno le soluzioni positive, se è <0 si prenderanno solo le soluzioni negative.
Per rendere più semplice tutto questo discorso facciamo un esempio.

Poniamo numeratore e denominatore >0. Otteniamo:
N: 2x² +x >0
D: x² – 9 >0
A questo punto li vado a calcolare separatamente.
N: 2x² +x >0 quindi considero l’equazione associata, però prima metto in evidenza:
x(2x + 1)=0 le soluzioni sono x= 0 e 2x +1=0⇒ x= – 1\2 .
Considerando che il Δ>0 e la disequazione è >0 le soluzioni sono esterne quindi x <- 1\2 e x>0.
N: x <-1\2 e x>0.
D: x² – 9 >0, l’equazione associata è x² – 9=0 ⇒ x²=9 ⇒ x=±3 . Anche in questo caso le soluzioni sono esterne quindi x< -3 e x>3
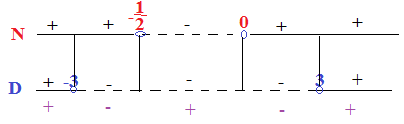
A questo punto riportiamo le soluzioni sul grafico per effettuare la regola dei segni.
A questo punto andiamo a vedere il segno della disequazione di partenza che è <0, quindi le soluzioni da considerare sono quelle negative e cioè -3<x<-1\2 e 0<x<3 .
Il pallino vuoto che si vede sul grafico indica che la disequazione non è anche uguale ,se fosse anche uguale il pallino sarebbe pieno.