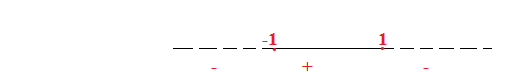Esercizi sulle disequazioni con valore assoluto
Svolgi le seguenti disequazioni.
1)|1 – x²| – x < x – 2
2)|x² -3x +2| > 2
3)x – |-x² + 2x| <3x -9
4)
5)
SVOLGIMENTO
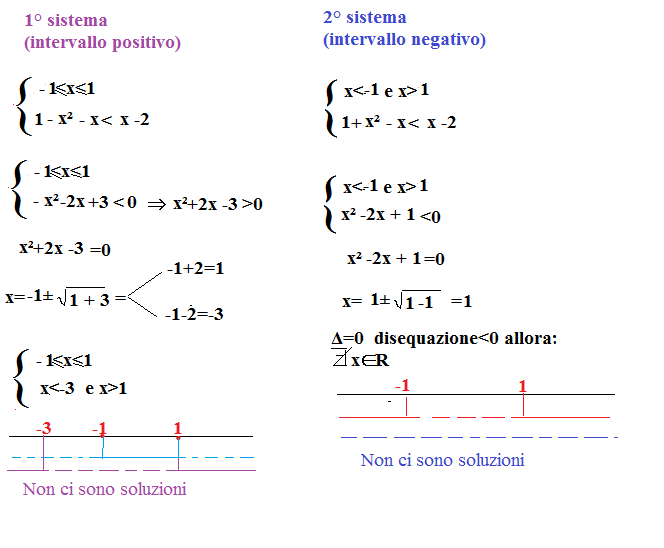
1)|1 – x²| – x < x – 2
Andiamo a studiare il segno dell’espressione che c’è all’interno del valore assoluto.
1 – x²≥ 0 quindi x²≤1 . Considerando l’equazione associata otteniamo x=±1 quindi poichè la disequazione è minore di zero e il delta maggiore di zero, le soluzioni saranno interne quindi: -1≤x≤1.
Quindi l’espressione del valore assoluto è positiva per -1≤x≤1. e negativa per x<-1 e x>1.
A questo punto consideriamo i due sistemi che otteniamo:
La nostra disequazione non ha soluzioni.
2)|x² -3x +2| > 2 studiamo il segno dell’espressione all’interno del valore assoluto
x² -3x +2≥0 Δ = 9-8 = 1
e
delta maggiore di zero, disequazione maggiore di zero, soluzioni esterne, quindi: x≤1 e x≥ 2 . Quest’ultimo è l’intervallo positivo, invece 1<x<2 è l’intervallo negativo.
A questo punto facciamo due sistemi, uno con le soluzioni dell’intervallo positivo e uno con quelle dell’intervallo negativo.
La disequazione iniziale non ha soluzioni.
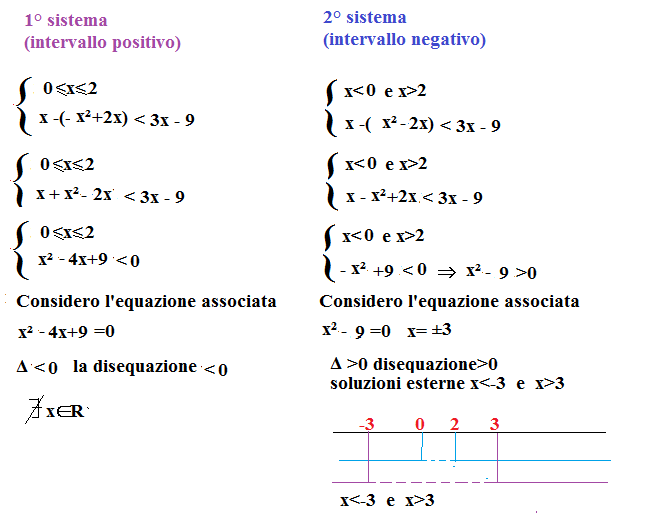
3)x – |-x² + 2x| <3x -9 studiamo il segno dell’espressione all’interno del valore assoluto
-x² + 2x≥0 ⇒ x² – 2x≤0 ⇒ x(x-2)≤0 quindi considerando l’equazione associata abbiamo che x=0 e x=2.
Poichè il delta è maggiore di zero e la disequazione è minore di zero allora le soluzioni saranno interne 0≤x≤2. Quest’ultimo è l’intervallo positivo, invece l’intervallo negativo e a x<0 e x>0
A questo punto facciamo due sistemi, uno con le soluzioni dell’intervallo positivo e uno con quelle dell’intervallo negativo.
La soluzione della disequazione è x<-3 e x>3.
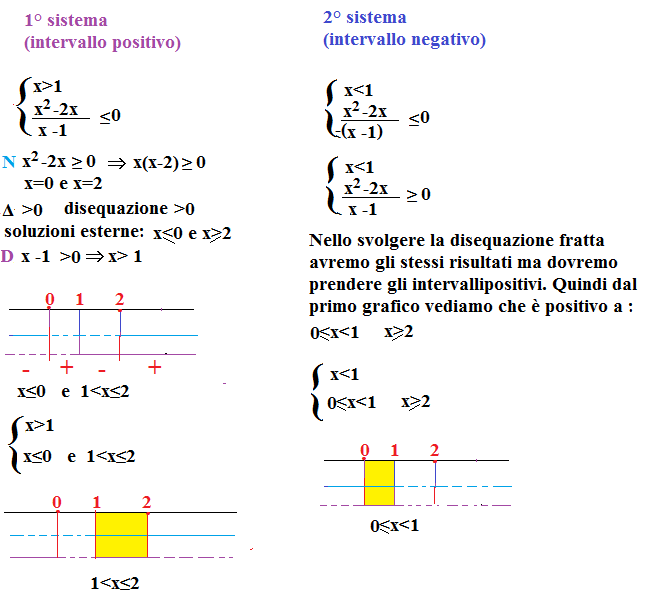
4)
studiamo il segno dell’espressione all’interno del valore assoluto
x-1>0 quindi x >1 sarà l’intervallo positivo e x <1 l’intervallo negativo. Lo possiamo vedere anche graficamente.
La disequazione iniziale ha come soluzione l’unione dei risultati di entrambe i sistemi, quindi 0≤x≤2 con x≠1.
5)
studiamo il segno dell’espressione all’interno del valore assoluto
2x>0 quindi x >0 che è l’intervallo positivo, mentre x<0 è l’intervallo negativo.
La soluzione della nostra disequazione con valore assoluto sarà data dall’unione tra x>1\2 e x>- 1\2.