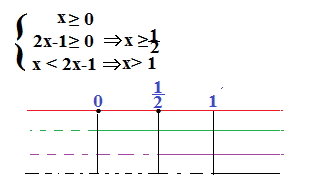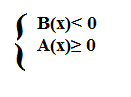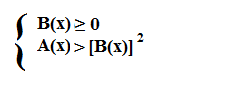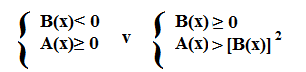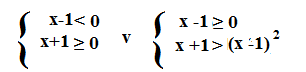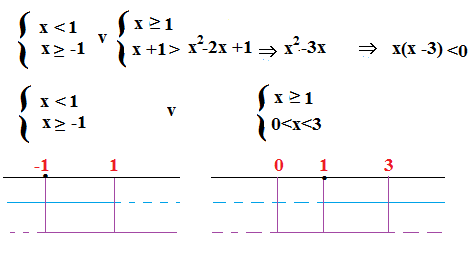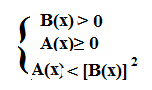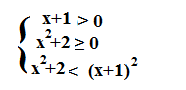Le disequazioni irrazionali contengono l’incognita sotto il segno di radice. Queste, come le equazioni irrazionali, si svolgono eliminando la radice con l’uso dell’elevamento a potenza.
Se l’indice è dispari, non bisogna porre alcuna condizione, quindi le soluzioni che si ottengono sono tutte accettabili. Se invece l’indice della radice è pari, bisogna fare la condizione di esistenza dei radicandi.
Consideriamo le varie situazioni che si possono venire a creare:
1° Situazione
oppure
A(x) e B(x) sono polinomi nell’incognita x.
Per la condizione di esistenza deve essere A(x)≥0 e B(x)≥0
A questo punto per risolvere la disequazione si elevano a quadrato entrambe i membri e si verifica se le soluzioni sono compatibili con la condizione di accettabilità.
Esempio:
La soluzione della disequazione è quindi x >1.
2° Situazione
Prima di tutto per l’esistenza della radice quadrata si deve porre il radicando, cioè A(x)≥ 0. A questo punto abbiamo due possibilità, perchè B(x) può essere sia positivo che negativo. Quindi esaminiamo i due casi: B(x)≥ 0 e B(x)<0.
Se B(x)<0 ed è soddisfatta la condizione A(x)≥ 0, allora la disequazione è verificata ed è equivalente al sistema:
Se B(x)≥ 0, possiamo elevare al quadrato entrambe i membri della disequazione, ottenendo:
Quindi possiamo dire che l’insieme delle soluzioni della disequazione irrazionale è dato dall’unione dell’insieme delle soluzione dei due sistemi quindi:
Facciamo un esempio:
A questo punto dobbiamo risolvere i due sistemi:
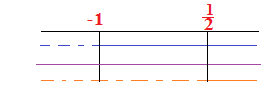
-1≤x< 1 1≤ x < 3
La disequazione iniziale è verificata dall’unione degli intervalli trovati , che alla fine sarà -1≤x<3.
3° Situazione
Poichè la radice è sempre positiva, per essere più piccola di B(x), vorrà dire che bisogna porre B(x)>0, oltre alla condizione di esistenza A(x)≥0.
Se le due condizioni sono verificate, quindi entrambe non saranno negative, possiamo elevare entrambe i membri al quadrato. Quindi una disequazione di questo tipo si risolverà con un solo sistema:
Facciamo un esempio:
A questo punto risolviamo il sistema:
La soluzione del sistema e quindi della disequazione è