Data la divisione A(x) : (x-a), il resto è dato dal valore che assume A(x) quando alla variabile si sostituisce il valore di a. Adesso dimostriamo il teorema del resto che ci permette di dire subito quale sia il risultato.
Dimostrazione
Data la divisione A(x) : (x-a), possiamo scrivere:
A(x)= (x-a) Q(x) + R Q(x) è il quoziente R è il resto
Sostituendo ad x il valore di a, otteniamo:
A(a)= (a-a)Q(a) + R
Essendo a-a=o, il prodotto (a-a)Q(a) si annulla, quindi A(a)=R
Per esempio se consideriamo il polinomio 5x² – 3x + 7 : x-2 con Ruffini avremo:
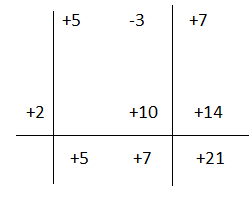
Il resto è 21.
Calcoliamo ora secondo il teorema del resto il valore che otteniamo sostituendo il valore x=2 cioè l’opposto del termine noto del divisore.
5x² – 3x + 7 = 5(2)² – 3(2) + 7 = 20 – 6 +7 = 21
Quindi per calcolare il resto si può non fare la divisione.