Boyle studiò che in condizioni di temperatura costante cioè isoterma , se comprimeva una certa quantità di aria portandola alla metà del suo volume, la pressione raddoppiava, riducendola di un terzo, triplicava e così via. Questa osservazione portò alla formulazione della legge di Boyle o legge isoterma:
A temperatura costante , per una determinata quantità di gas , il volume è inversamente proporzionale alla pressione. p • V= k
Il valore di tale costante, a parità di temperatura e di quantità di gas, è uguale per tutti i gas che hanno un comportamento ideale.
Per capire meglio come Boyle arrivò a tali considerazioni, prendiamo una siringa e aspiriamo un po’ d’aria da essa, chiudiamo l’estremità aperta con un dito e comprimiamo lo stantuffo, vedremo che il volume occupato dall’aria diminuisce. Una volta rilasciato lo stantuffo, lo stantuffo ritorna alla posizione iniziale e quindi il volume aumenta di nuovo..
Consideriamo il caso che per un gas abbiamo due diverse condizioni di pressione e
e due volumi
e
, possiamo scrivere la relazione come. Se consideriamo la legge di Boyl abbiamo:
e
Poichè il numero di particelle è lo stesso, come anche la temperatura allora il valore della k è lo stesso quindi possiamo eguagliare le due equazioni.
Con questa nuova equazione è possibile determinare il valore di ognuna delle grandezze che vi compaiono, noti i valori delle altre tre:
oppure
e
e infine
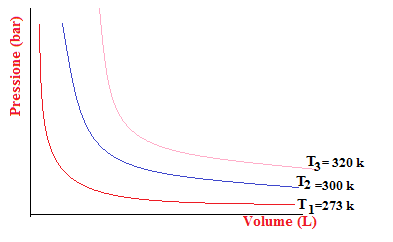
Se si riportano su un sistema di assi ortogonali i valori della pressione e del volume, dove sull’ordinata si pone la pressione e sull’ascissa il volume. Si nota la formazione di una curva detta isoterma, corrispondente al ramo di un’iperbole equilatera (caratteristico della relazione della proporzionalità inversa).
Ogni volta che si ripete l’esperimento si nota che l’iperbole si allontana dall’origine degli assi.