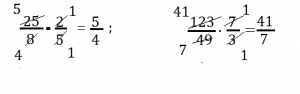MOLTIPLICAZIONE
Il prodotto di due o più frazioni è la frazione avente come numeratore il prodotto dei numeratori e per denominatore il prodotto dei denominatori.
Le moltiplicazioni di frazioni godono di tutte le proprietà delle moltiplicazioni dei numeri naturali, è una operazione sempre possibile nell’insieme dei numeri frazionari e l’elemento neutro è l’unità.
Infatti :
INVERSO O RECIPROCO
Due frazioni si dicono inverse o reciproche se il loro prodotto è uguale a 1.
Data una frazione con un numeratore diverso da zero, la sua inversa o reciproca si ottiene scambiando il numeratore con il denominatore.
5\9 è l’inverso di 9\5
DIVISIONE
Il quoziente di due frazioni, di cui la seconda diversa da zero, è la frazione che si ottiene moltiplicando la prima per l’inverso della seconda.
Esempi:
ma dividendo numeratore e denominatore per 4 avremo 2\9
10 lo dividiamo per 5 e 21 lo dividiamo per 7
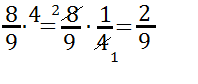
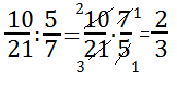
POTENZA
La potenza di una frazione è una frazione avente per numeratore la potenza del numeratore e per denominatore la potenza del denominatore.
Le proprietà delle potenze dei numeri naturali sono valide anche per le potenze delle frazioni.
Se scrivessimo senza parentesi avremmo
Il risultato di una potenza è negativo solo in caso di frazione negativa ed esponente negativo come .
Potenze a esponente negativo: la potenza di un numero razionale, diversa da zero, con esponente intero negativo è una potenza che ha per base il reciproco del numero dato e per esponente l’opposto dell’esponente.
Per esempio
; ;
