Relazione di equivalenza e partizione
Una relazione che gode della proprietà riflessiva, simmetrica e transitiva si dice relazione di equivalenza.
Consideriamo l’insieme A:

e consideriamo la relazione:
ℜ = “… ha la stessa forma… ”
La relazione ℜ è una relazione di equivalenza in quanto sono verificate le proprietà:
- riflessiva: ogni figura è in relazione con se stessa;
- simmetrica: se una figura ha la stessa forma di un’altra, quest’ultima ha la stessa forma della prima;
- transitiva: se una figura ha la forma di un’altra, e questa la stessa forma di una terza, la prima e la terza figura hanno la stessa forma.
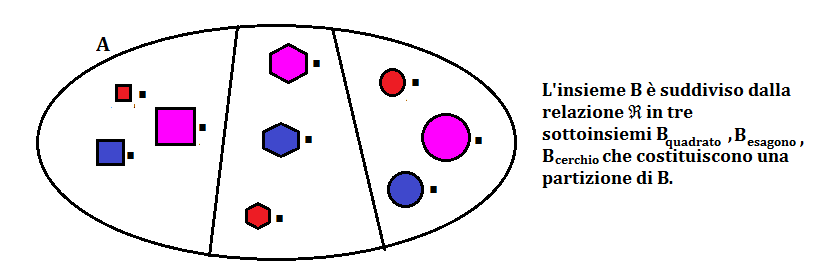
Questi sottoinsiemi sono detti classi di equivalenza perchè gli elementi della classe sono equivalenti fra loro relativamente alla forma: se si vuole una figura quadrata si può scegliere indifferentemente.
In pratica, la relazione di equivalenza ci permettono di classificare gli oggetti in base a una loro proprietà.
L’insieme i cui elementi sono le classi di equivalenza si chiama insieme quoziente. Dunque l’insieme quoziente è un insieme di sottoinsieme.
La relazione di equivalenza è uno dei tipi di relazione più usato, sia nel vivere quotidiano, sia in matematica.