RETTE PASSANTI PER L’ORIGINE
Un’equazione di primo grado in due incognite del tipo y=mx, dove m è un numero reale fissato, descrive una retta passante per l’origine.
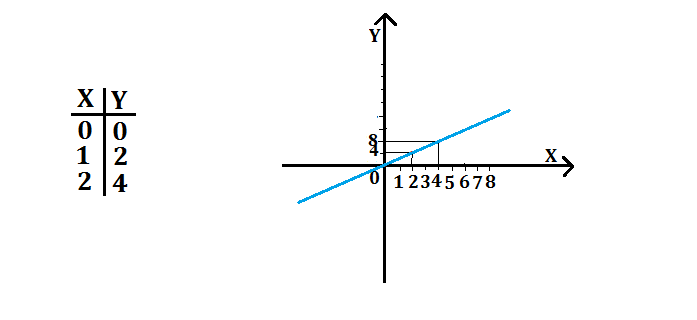
Per esempio y=2x per poterlo disegnare si attribuiscono dei valori alla x ottenendo così il valore della y. Per disegnarla con più precisione si danno altri valori così si ottengono più coppie di coordinate.
Tale retta passerà per l’origine perchè se x=0 vorrà dire che andando a sostituire la x nell’equazione della retta y=2x avremo che anche la y=0 quindi; O(0,0)
L’ascissa ha quindi il ruolo di variabile indipendente e l’ordinata della variabile dipendente.
Esercizio n° 1
Disegna il grafico e riconosci le caratteristiche di ciascuna funzione del tipo y = mx
a) y = + 
x
Per costruire la tabella dei valori conviene attribuire alla x valori multipli di 3 in modo da far scomparire il denominatore.
| x | -6 | -3 | 0 | +3 | +6 |
| y | -10 | -5 | 0 | +5 | +10 |
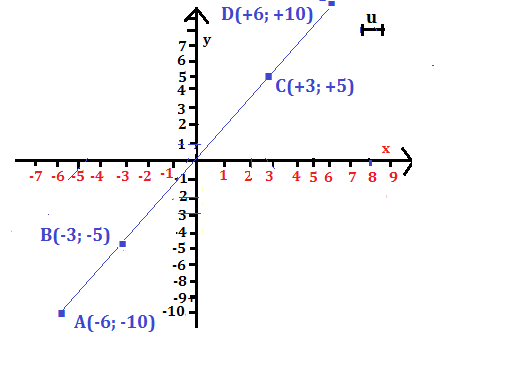
Otteniamo così i punti A ( -6 ; 10), B(-3; -5), O (0,0), C (+3; +5), D (+6; +10).
La rappresentazione grafica è:
La funzione è una retta passante per l’origine degli assi; il coefficiente angolare è m= + ;
essendo m > 0, i quadranti attraversati sono il primo e il terzo.
b) y = -2x
La tabella dei valori è:
| x | -2 | -1 | 0 | +1 | +2 |
| y | +4 | +2 | 0 | -2 | -4 |
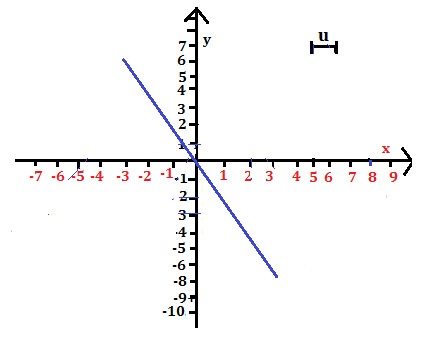
La rappresentazione grafica è:
La funzione è una retta passante per l’origine degli assi; il coefficiente angolare è m = -2;
essendo m < 0, i quadranti attraversati sono il secondo e il quarto.
Esercizio n° 2
Con riferimento a ciascun grafico, scrivi l’equazione delle rette r ed s rappresentate.
a)
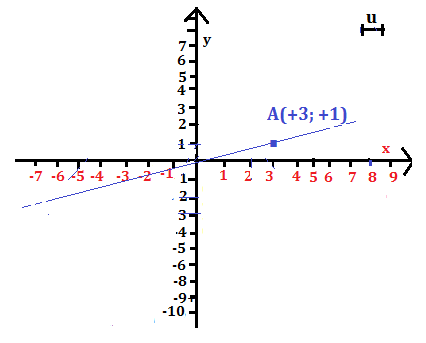
La retta r passa per l’origine O, quindi la sua equazione è del tipo y = mx, dove m = , (rapporto fra l’ordinata e l’ascissa di un suo punto) per cui si ottiene: y = x
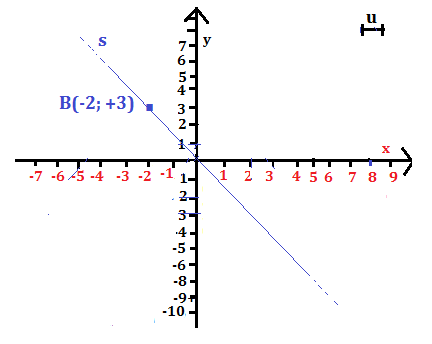
b)
La retta s è del tipo y = mx, dove m = = – , per cui si ottiene: y = – x.
