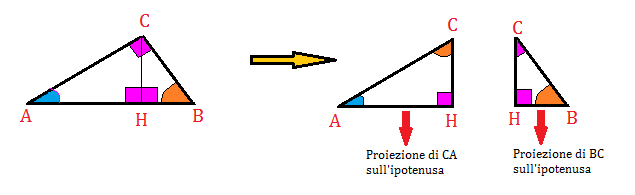
Consideriamo un triangolo rettangolo ABC rettangolo in C. Tracciamo l’altezza relativa all’ipotenusa e vediamo che risulterà diviso dall’altezza CH in due triangoli rettangoli AHC e HBC simili ad ABC, avendo gli angoli congruenti.
Il triangolo AHC e HBC essendo simili ad ACB per il primo teorema di Euclide, sono simili tra loro, vale quindi la proporzione:
AH : CH = CH : HB
Osservando la proporzione possiamo enunciare il secondo teorema di Euclide.
In un triangolo rettangolo l’altezza relativa all’ipotenusa è media proporzionale tra le proiezioni dei cateti sull’ipotenusa stessa.
Esso si può enunciare anche diversamente, Considerando che AH : CH = CH : HB, otteniamo:
- CH² = AH x HB quindi:
Quindi possiamo affermare che:
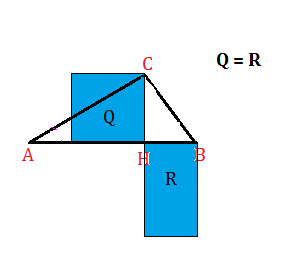
il quadrato costruito sull’altezza relativa all’ipotenusa è equivalente al rettangolo che ha per dimensioni le due proiezioni dei cateti sull’ipotenusa stessa.
Ecco la rappresentazione geometrica del secondo teorema di Euclide: