Il primo Teorema spiegato in modo semplice con esempi ed esercizi.
Consideriamo un triangolo rettangolo ABC rettangolo in C. Tracciamo l’altezza relativa all’ipotenusa e vediamo che risulterà diviso dall’altezza CH in due triangoli rettangoli AHC e HBC simili ad ABC, avendo gli angoli congruenti.
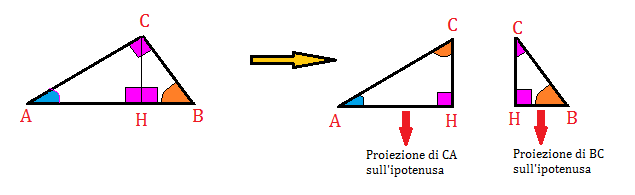
PRIMO TEOREMA DI EUCLIDE
Consideriamo i triangoli ABC e AHC disegnati sopra:

Consideriamo i triangoli ABC e CBH disegnati sopra:
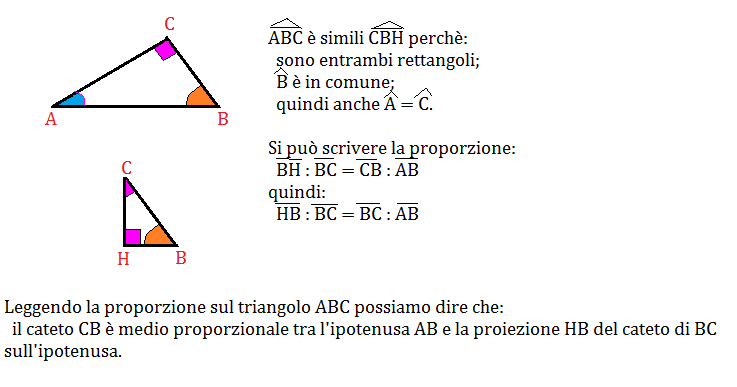
In un triangolo rettangolo un cateto è medio proporzionale fra l’ipotenusa e la proiezione del cateto sull’ipotenusa.
Tale teorema si può enunciare anche diversamente, infatti, dalle proporzioni:
AH : CA = CA : AB HB : BC = BC : AB
Applicando la proprietà fondamentale delle proporzioni, otteniamo:
- CA² = AH x AB quindi
- BC² = HB x AB quindi
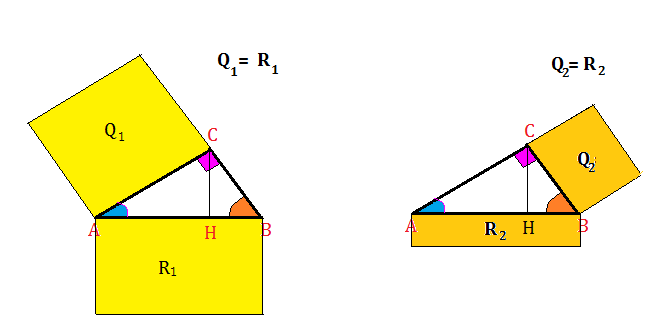
Il teorema di Euclide lo si può enunciare anche così:
il quadrato costruito su un cateto è equivalente al rettangolo che ha per dimensioni l’ipotenusa e la proiezione del cateto sull’ipotenusa.
Ecco la rappresentazione geometrica: