Esercizi sulle equazioni parametriche.
Esercizio n° 1
Determina per quali valori del parametro k l’equazione
x² – (k +1)x + 1=0
ammette due soluzioni reali e coincidenti.
Esercizio n° 2
Determina per quali valori del parametro k l’equazione
x² – 5kx + 2k – 3=0
ha una soluzione x=2
Esercizio n° 3
Determina per quali valori del parametro k l’equazione
3x² – 5x + k – 6 =0
ammette due soluzioni reciproche
Esercizio n° 4
Determina per quali valori del parametro k l’equazione
3x² + (2k – 1)x + k – 2 =0
ammette due soluzioni la cui somma è 13
Esercizio n° 5
Data l’equazione parametrica
kx² + 2(k + 1)x + k + 1 =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le due soluzioni sono reali e distinte;
b) una delle soluzioni è x=0;
c) la somma delle soluzioni è uguale a -8;
d) il prodotto delle soluzioni è maggiore di 2.
Esercizio n° 6
Data l’equazione parametrica
3x² – 2(3k + 2)x +8k =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le soluzioni sono reali e distinte;
b) una radice è uguale a 1.
Esercizio n° 7
Data l’equazione parametrica
kx² – (2k – 1)x + k – 3 =0 con k≠0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) la somma delle radici è minore di 2;
b) il prodotto delle radice è uguale a 4.
Esercizio n° 8
Data l’equazione parametrica
(k-1)x² -2 (k + 1)x + k +3 =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) la somma delle radici è positiva;
b) il prodotto delle radici è negativo;
Esercizio n° 9
Data l’equazione parametrica
mx² +2 (3 – m)x -12 =0 con m≠0
determina per quali valori del parametro m sono verificate le seguenti condizioni:
a) le radici sono reali;
b) le radici sono uguali;
c) le radici sono opposte;
d) le radici sono reciproche;
e) una radice è nulla.
Esercizio n° 10
Data l’equazione parametrica
x² -2 (k – 2)x +k² – 3k =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le soluzioni non sono reali;
b) una radice è nulla;
c) il prodotto è negativo;
d) la somma dei quadrati delle radici è uguale a 4.
Esercizio n° 11
Data l’equazione parametrica
(k² -1 ) x² -4kx + 4=0 con k≠±1
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le radici sono reali e distinte;
b) le radici sono uguali;
c) le radici sono opposte;
d) le radici sono reciproche;
e) la somma dei reciproci delle radici è uguale a 12.
SVOLGIMENTO
Esercizio n° 1
Determina per quali valori del parametro k l’equazione
x² – (k +1)x + 1=0
ammette due soluzioni reali e coincidenti.
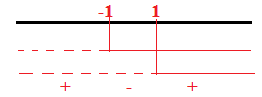
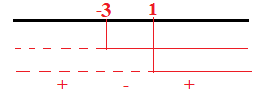
Si pone il Δ=0 ma il Δ=b² – 4ac quindi Δ=(k + 1) ² – 4 quindi k² + 1+ 2k – 4=0
k² + 2k – 3=0 a questo punto calcoliamoci la k con la formula ridotta
k= -1 ± = -1 ± 2
= 1;
= -3
Esercizio n° 2
Determina per quali valori del parametro k l’equazione
x² – 5kx + 2k – 3=0
ha una soluzione x=2.
Si sostituisce 2 alle x dell’equazione, ottenendo:
4 – 10k + 2k – 3=0
-8k + 1 =0 ⇒ k= 1\8
Esercizio n° 3
Determina per quali valori del parametro k l’equazione
3x² – 5x + k – 6 =0
ammette due soluzioni reciproche.
Quindi = 1\
cioè
•
= 1
sappiamo che il prodotto delle radici corrisponde a c\a quindi abbiamo:
c\a= 1 andiamo a sostituire i dati dell’equazione cioè c= k – 6 e a=3.
⇒ k – 6 = 3 ⇒ k= 9
Esercizio n° 4
Determina per quali valori del parametro k l’equazione
3x² + (2k – 1)x + k – 2 =0
ammette due soluzioni la cui somma è 13.
Quindi +
= 13 poichè la somma è uguale a – b\a possiamo scrivere anche:
-b\a= 13 dove b= 2k – 1 ed a= 3
quindi
facciamo il minimo comune divisore
⇒ -2k + 1 = 39⇒ -2k = 38quindi k= -19
Esercizio n° 5
Data l’equazione parametrica
kx² + 2(k + 1)x + k + 1 =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le due soluzioni sono reali e distinte;
b) una delle soluzioni è x=0;
c) la somma delle soluzioni è uguale a -8;
d) il prodotto delle soluzioni è maggiore di 2.
SVOLGO
a) si pone il Δ >0, poichè il coefficiente della x è un numero pari facciamo il Δ\4.
Δ\4 = (k +1)² -k(k+1)
(k +1)² -k(k+1) >0 ⇒ k² + 1 + 2k – k² – k >0 ⇒ k + 1 >0 quindi k > – 1
b) vuol dire che x=0 , quindi vado a sostituire lo 0 nelle x e ottengo:
0 + 0 + k +1=0 ⇒ k= -1
c) +
= – 8 poichè la somma è uguale a – b\a possiamo scrivere anche:
-b\a= – 8 quindi andando a sostituire visto che a= k e b= 2(k+1)
C.E. K ≠ 0
⇒ -2k – 2 =-8k ⇒ 6k = 2 quindi k = 1\3
d) •
>2 quindi c\a>2 andando a sostituire c= k+1 ed a = k otteniamo:
k+1>2 ⇒ k > 1
k > 0
a questo punto facciamo un falso sistema tra:
Si prendono le soluzioni positive quindi x< 0 e x >0
Esercizio n° 6
Data l’equazione parametrica
3x² – 2(3k + 2)x +8k =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le soluzioni sono reali e distinte;
b) una radice è uguale a 1.
SVOLGO
a) Si pone il Δ >0, visto che il coefficiente della x è pari, allora facciamo il Δ \4= (3k + 2)² – 24
3k² + 12k + 4 – 24 >0 ⇒ 3k² + 12k + 28 >0 a questo punto ci calcoliamo i valori delle k con la formula ridotta, facendoci prima il Δ \4= 36 – 84 < 0 quindi non esiste k ∈R.
b) x= 1, vado a sostituire l’uno alle x e ottengo:
3 – 2(3k +2)1 + 8k =0 ⇒ 3 – 6k – 4 + 8k =0 ⇒ 2k – 1 = 0 quindi k=1\2
Esercizio n° 7
Data l’equazione parametrica
kx² – (2k – 1)x + k – 3 =0 con k≠0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) la somma delle radici è minore di 2;
b) il prodotto delle radice è uguale a 4.
SVOLGO
a) +
< 2 quindi – b\a< 2 e sostituendo otteniamo:
facciamo il minimo comune divisore e otteniamo:
al numeratore va via la k e rimane -1> 0 è impossibile quindi sul grafico sarà tratteggiato
il denominatore k> 0 quindi
la parte negativa sarà proprio k> 0
b) •
= 4 quindi c\a =4 sostituendo otteniamo:
C.E. k≠ 0
quindi k – 3 =4k ⇒ 3k = -3 qundi k = -1 che non è accettabile perchè non è reale.
Esercizio n° 8
Data l’equazione parametrica
(k-1)x² -2 (k + 1)x + k +3 =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) la somma delle radici è positiva;
b) il prodotto delle radici è negativo;
SVOLGO
a) +
>0 quindi – b\a>0 andando a sostituire otteniamo:
svolgiamo un falso sistema tra:
k + 1 >0 ⇒ k> -1
k – 1 >0 ⇒ k > 1
si prendono le soluzioni positive quindi k< -1 e k > 1
b) •
< 0 quindi c\a< 0 , andando a sostituire otteniamo:
svolgiamo un falso sistema tra:
k+3 >0 ⇒ k > -3
k – 1 >0 ⇒ k > 1
si prendono le soluzioni negative quindi -3 < x < 1
Esercizio n° 9
Data l’equazione parametrica
mx² +2 (3 – m)x -12 =0 con m≠0
determina per quali valori del parametro m sono verificate le seguenti condizioni:
a) le radici sono reali;
b) le radici sono uguali;
c) le radici sono opposte;
d) le radici sono reciproche;
e) una radice è nulla.
SVOLGO
a) si pone Δ ≥ 0, visto che il coefficiente della x è pari facciamo il Δ\4
m² + 6m + 9 ≥ 0 ⇒ il Δ\4 = 9 – 9 quindi Δ=0 , disequazione ≥ 0 quindi la soluzione è per ogni x ∈R.
b) =
quindi poniamo Δ= 0 , visto che il coefficiente della x è pari facciamo il Δ\4 = 9 – 9 =0 quindi
-(3-m )± 0 quindi -3 + m =0 ⇒ m = 3
c) = –
⇒
+
= 0 quindi -b\a = 0 sostituendo otteniamo:
C.E. m≠ 0
⇒ – 6 + 2m = 0 ⇒ m = 3
d)
cioè •
= 1 sostituendo otteniamo:
c\a =1 ⇒ – 12\m=-1 ⇒ m = -12
e) x= 0 quindi sostituisco lo 0 alle x e ottengo:
0 + 0 – 12 = 0 quindi è impossibile e non esistono m ∈ R
Esercizio n° 10
Data l’equazione parametrica
x² -2 (k – 2)x +k² – 3k =0
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le soluzioni non sono reali;
b) una radice è nulla;
c) il prodotto è negativo;
d) la somma dei quadrati delle radici è uguale a 4.
SVOLGO
a) Δ<0 , visto che il coefficiente della x è pari facciamo il Δ\4 = (k – 2)² – (k² – 3k)
(k – 2)² – (k² – 3k) <0 ⇒ k² + 4 – 4k – k² + 3k <0 ⇒ -k < – 4 ⇒ k > 4
b) x=0, sostituiamo lo 0 alle x e otteniamo:
0 – 0 + k² -3k =0 quindi k(k – 3)=0 le soluzioni sono k=0 e k=3
c) •
< 0 quindi c\a < 0
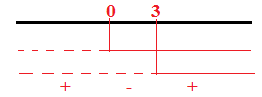
k² – 3k < 0 quindi k(k – 3) < 0 faccio il falso sistema tra:
k> 0
k – 3> 0 quindi k > 3
Si prendono le soluzioni negative quindi 0<k< 3.
d)
quindi si pone
quindi più semplicemente
[ 2(k -2)]² – 2(k² – 3k) = 16
[ 2k – 4]² -2k² + 6k = 16
4k² + 16 – 16k – 2k² + 6k = 16
2k² – 10k =0 ⇒ 2k( k – 5) =0
le soluzioni sono k=0 e k=5, ma k=5 non è accettabile perchè per k> 4 le soluzioni non sono reali
Esercizio n° 11
Data l’equazione parametrica
(k² -1 ) x² -4kx + 4=0 con k≠±1
determina per quali valori del parametro k sono verificate le seguenti condizioni:
a) le radici sono reali e distinte;
b) le radici sono uguali;
c) le radici sono opposte;
d) le radici sono reciproche;
SVOLGO
a)Δ > 0, poichè il coefficiente della x è pari facciamo il = 4k² – 4(k² – 1)
4k² – 4k² + 4 >0 per ogni k ∈ R
b) =
quindi Δ = 0 4=0 è impossibile quindi non esiste k ∈ R
c)= –
⇒
+
=0 quindi – b\a =0 andando a sostituire otteniamo:
C.E. K²-1≠ 0
quindi k=0
d)
cioè •
= 1 sostituendo otteniamo:
c\a =1 ⇒
⇒ 4= k² – 1 ⇒ k² = 5 svolgendola otteniamo k = ±
Programma di matematica secondo superiore