Esercizi sulla retta di geometria analitica in modo da esercitarsi e capire bene quest’argomento che ritornerà spesso durante il corso di studio.
ESERCIZIO N° 1
Determina l’equazione della retta passante per l’origine e per il punto A(1\2; 2\5). Verifichiamo inoltre se i punti B(5\4; 1) e C(2; 5) appartengono a tale retta.
ESERCIZIO N° 2
Scrivi l’equazione della retta , passante per l’origine e per il punto A. Verifica se il punto B appartiene alla retta.
- A(-2 ; 0) B(-2; 10)
- A(3; 2) B(6; 4)
ESERCIZIO N° 3
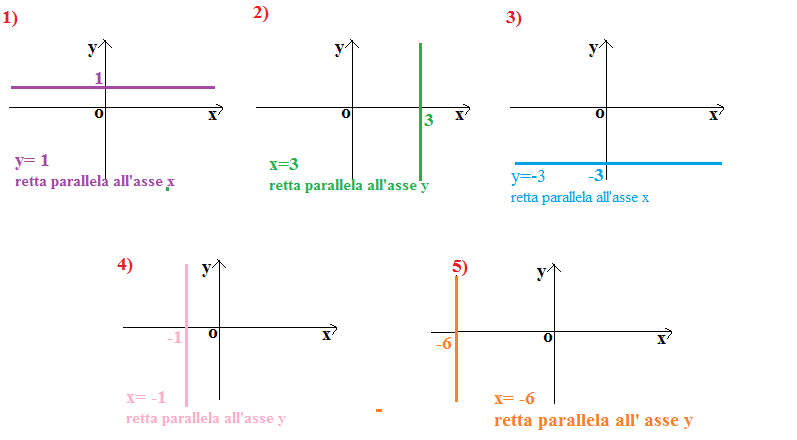
Scrivi l’equazione delle rette disegnate nei grafici.
ESERCIZIO N° 4
Scrivi in forma implicita le seguenti equazioni.
y = 4x + 8; y= 1 – 2x ; y= 3\4x – 2\3; y= 3\5x; y=- 1\5x + 2\3; y= -1\2x + 3\4
ESERCIZIO N° 5
Scrivi in forma esplicita le seguenti equazioni.
3x-y + 3=0; 4x+2y= 0; -2x + 5y = -1; x + y – 1 =0
ESERCIZIO N° 6
In ciascuno dei seguenti casi, verifica se il punto P appartiene alla retta data.
1)P(3; 4) r: 3x – 2y = 1
2)P(0; 10) r: 1\2y + 2x =5
3)P(1; 1\2) r: 3x – y + 1 =0
SVOLGIMENTO
ESERCIZIO N° 1
Determina l’equazione della retta passante per l’origine e per il punto A(1\2; 2\5). Verifichiamo inoltre se i punti B(5\4; 1) e C(2; 5) appartengono a tale retta.
Poichè la retta che passa per l’origine ha equazione y=mx , vorrà dire che m=y\x quindi
La retta cercata è y= 4\5x
Per verificare se i punti appartengono alla retta li andiamo a sostituire uno alla volta.
Verifichiamo prima B(5\4; 1) , dall’equazione y= 4\5x otteniamo ⇒ 1=1 quindi il punto B appartiene alla retta.
Verifichiamo ora C(2; 5),dall’equazione y= 4\5x otteniamo 5=4\5• 2 ⇒ 5= 8\5 quindi C non appartiene alla retta.
ESERCIZIO N° 2
Scrivi l’equazione della retta , passante per l’origine e per il punto A. Verifica se il punto B appartiene alla retta.
- A(-2 ; 0) B(-2; 10)
- A(3; 2) B(6; 4)
1)A(-2; 0)
passante per l’origine quindi y= mx ⇒ m=y\x quindi m = 0 perchè y è uguale a 0. La retta cercata è y=0.
Il punto B(-2; 10) non appartiene alla retta lo si capisce senza effettuare sostituzioni perchè y non è zero.
2)A(3; 2)
Passa per l’origine quindi l’equazione è y= mx ⇒ m=y\x quindi m= 2\3. La retta sarà y = 2\3x.
Per vedere se il punto B appartiene alla retta andiamo a sostituire le sue coordinate nella retta e otteniamo 4 = 2\3•6.
Quindi 4=4, ciò vuol dire che il punto appartiene alla retta.
ESERCIZIO N° 3
Scrivi l’equazione delle rette disegnate nei grafici.
ESERCIZIO N° 4
Scrivi in forma implicita le seguenti equazioni.
y = 4x + 8; y= 1 – 2x ; y= 3\4x – 2\3; y= 3\5x; y=– 1\5x + 2\3; y= -1\2x + 3\4
y = 4x + 8 ⇒ 4x – y + 8 =0
y= 1 – 2x ⇒ 2x + y – 1 =0
y= 3\4x – 2\3 si fa il minimo comune multiplo che è 12 quindi avremo 12y = 9x -8 ⇒ 9x – 12y -8=0
y= 3\5x ⇒ 5y = 3x ⇒ 3x – 5y =0
y=- 1\5x + 2\3 il minimo comune multiplo è 15 quindi 15y = – 3x +10 ⇒ 3x+15y – 10=0
y= -1\2x + 3\4 il minimo comune multiplo è 4 quindi 4y = -2x + 3 ⇒ 2x + 4y – 3 = 0
ESERCIZIO N° 5
Scrivi in forma esplicita le seguenti equazioni.
3x-y + 3=0; 4x+2y= 0; -2x + 5y = -1; x + y – 1 =0
3x-y + 3=0 ⇒ y = 3x + 3
4x+2y= 0 ⇒ 2y = -4x ⇒ y = 4\2x ⇒ y = -2
-2x + 5y = -1 ⇒ 5y = 2x -1 ⇒ y = 2\5x – 1\5
x + y – 1 =0 ⇒ y = – x + 1
ESERCIZIO N° 6
In ciascuno dei seguenti casi, verifica se il punto P appartiene alla retta data.
1)P(3; 4) r: 3x – 2y = 1
Per verificare bisogna vedere se le coordinate del punto soddisfino l’equazione e quindi bisogna sostituirle alle incognite x e y.
3(3)-2(4)=1 ⇒ 9-8 = 1 ⇒ 1=1
P appartiene alla retta
2)P(0; 10) r: 1\2y + 2x =5
1\2•(10) + 2 (0) = 5 ⇒ 5 =5
P appartiene alla retta
3)P(1; 1\2) r: 3x – y + 1=0
3(1) – 1\2 = -1 ⇒ 3 – 1\2 = – 1 ⇒ 5\2 = -1
P non appartiene alla retta