Esercizi sull’intersezione e sull’unione
Esercizio n° 1
Dati gli insiemi A = {a / a è una lettera della parola casale} e B ={b / b è una lettera della parola sole}, rappresentare per elencazione e graficamente l’insieme intersezione.
Esercizio n° 2
Dati gli insiemi A = {Carlo, Rita, Paolo, Elena} e B = {Andrea, Franca, Veronica, Elisabetta}, rappresentare per elencazione e graficamente l’insieme intersezione.
Esercizio n° 3
Dati gli insiemi A = {a / a è una cifra del numero 135679} e B = {b / b è una cifra del numero 6793}, rappresentare per elencazione e graficamente l’insieme intersezione.
Esercizio n° 4
Dati gli insiemi A = {a, b, e, d, r} ; B = {a, b, e, c, d, s} ; C = {a, b, e, s, r, l}, rappresentare per elencazione e graficamente l’insieme intersezione.
Esercizio n° 5
Siano A={1,3,5} e B= {2,4}: determinare A ∩ B.
Esercizio n° 6
Siano A={a, b, c}, B= {a, d}, C= {c, a}. Rappresentare (A ∩ B) ∩ C e A ∩ (B∩ C).
Esercizio n° 7
Sia : A = {a, b, c, d}; B= {a, b, m, n}; indicare gli insiemi A ∩ B; (A ∩ B) ∩ A; (A ∩ B)∩ B.
Esercizio n° 8
Rappresentare l’insieme unione dell’insieme dei numeri dispari formati da una sola cifra con l’insieme dei numeri pari minori di 10.
Esercizio n° 9
Rappresentare graficamente gli insiemi A= {m, n, p, q}, B= {m, p, r}, A∪ B, A ∩ B.
Esercizio n° 10
Siano A= {x|x < 6, x ∈ N} e B = {x|x ≤ 6 x ≤ 7, x ∈ N}; determinare A∪ B e A ∩ B.
Esercizio n° 11
Consideriamo gli insiemi : A= {1, 2, 3}, B= {2, 4, 6}, C= {1, 3, 5} .
Determinare: A∪ B, B∪C, A∪( B∪C), (A∪ B)∪C, A ∩ B, B ∩ C, A ∩ ( B ∩ C), (A ∩ B)∩ C.
Esercizio n° 12
Determina l’intersezione e l’unione dei due insiemi:
A= {x|x è una lettera della parola “mare”}
B= = {x|x è una vocale}
Esercizio n° 13
Per ogni coppia di insiemi determina l’unione e l’intersezione, rappresentandole con diagramma di Eulero-Venn
A= {2, 5, 7, 12} B= {2, 3, 7, 11, 13}
C={7, 3, 2} D = {2, 3, 7, 11, 13}
E={17, 19, 23} F= {2, 3, 7, 11, 13}
G= {x|x è una lettera della parola “ventilatore”} H= {x|x è una lettera della parola “turbina”}
Esercizio n° 14
Determina l’intersezione e l’unione fra i seguenti insiemi di persone A e B.
A= {x|x ha una statura superiore a 1,30 m} B= {x|x ha una statura inferiore a 1,90 m}
A= {x|x ha più di 20 anni} B= {x|x ha meno di 20 anni}
Esercizio n° 15
Fornisci due esempi di insiemi disgiunti e rappresentali con diagrammi di Eulero-Venn.
Esercizio n° 16
Dati gli insiemi: A= {1, 2, 3, 4, 5}, B= {3, 4, 5, 6, 7}, C= {2, 4, 6, 8} .
Calcoliamo A∪( B∩C), (A∩B)∪C, A∩( B∩C), A∪( B∪C), (A∩B)∩C, (A∪B)∩C.
Esercizio n° 17
Dati gli insiemi : A= {0, 1, a}, B= {1, 2, a, b}, C= {0, 2, 4}, calcola i risultati delle seguenti espressioni.
A∩B∪C, A∪( B∩C), (A∪B)∩ (A∩C), A∪B∪C, (A∩B)∪ (A∩C), (A∪B)∩ (B∪C)
Esercizio n° 18
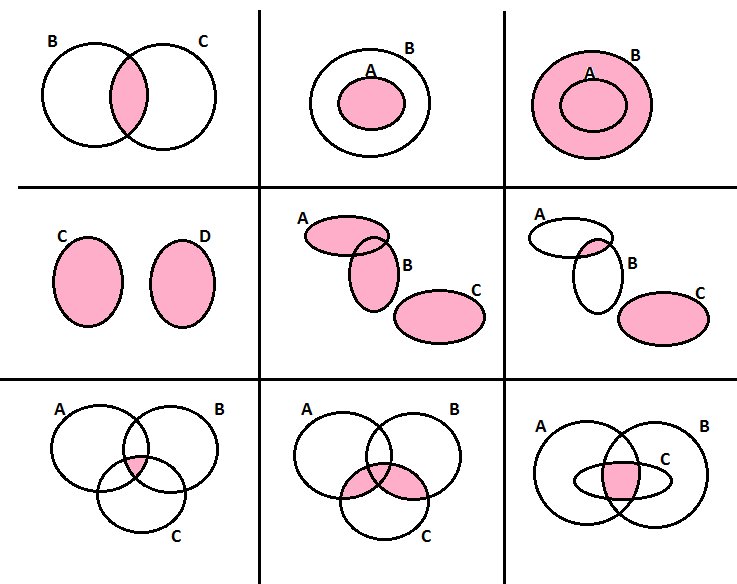
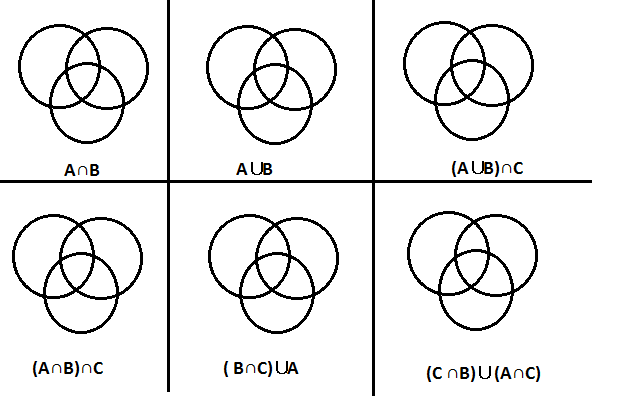
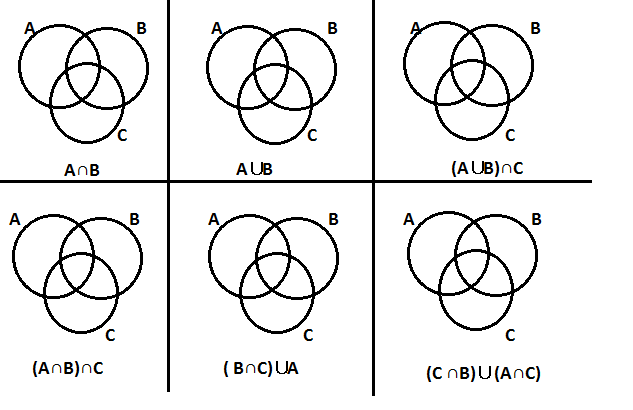
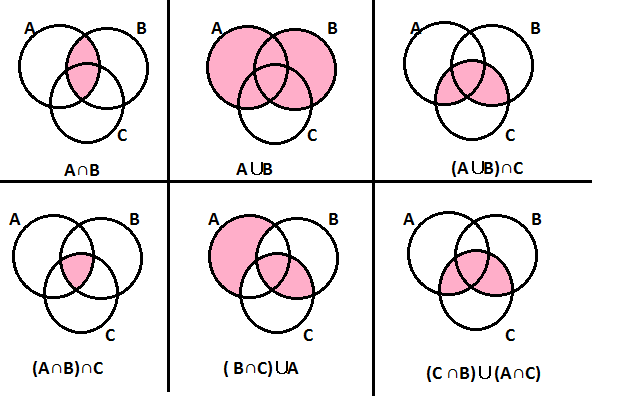
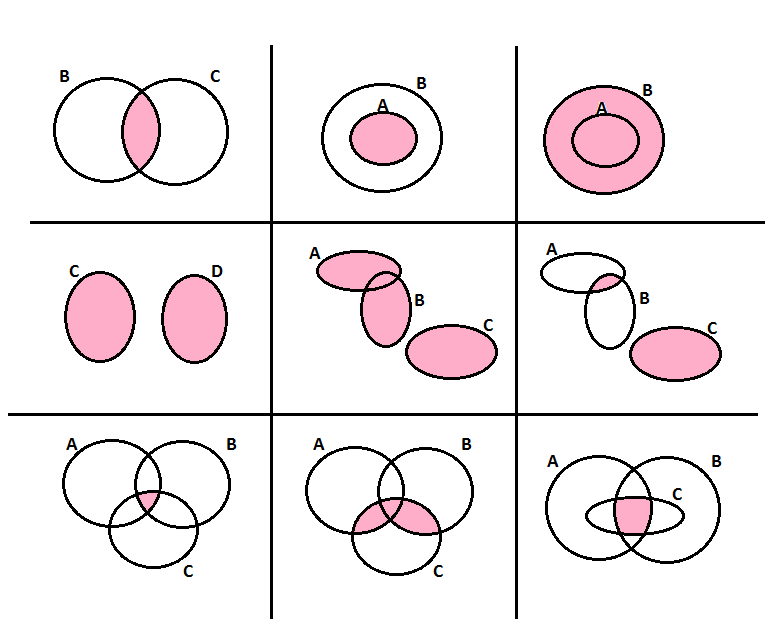
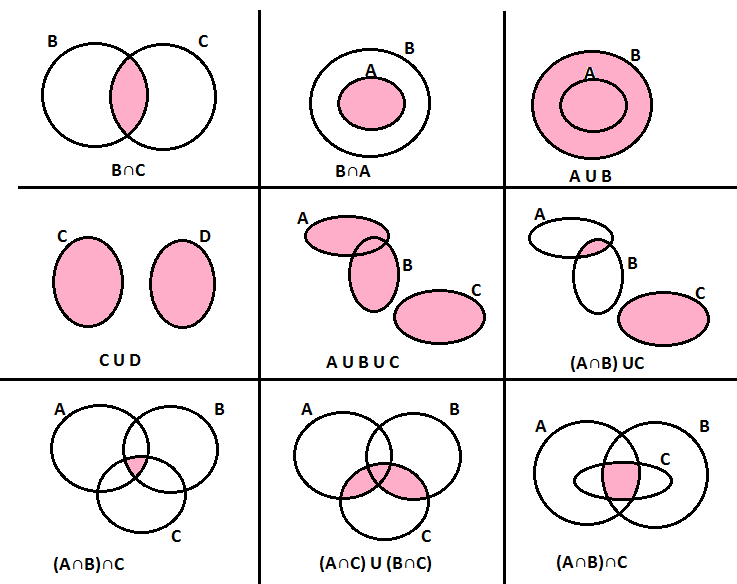
Esprimi mediante una espressione con l’unione e l’intersezione fra insiemi, la parte colorata in ognuno dei diagrammi delle figure seguenti.
Svolgimento
Esercizio n° 1
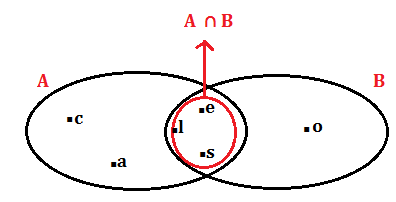
Dati gli insiemi A = {a / a è una lettera della parola casale} e B ={b / b è una lettera della parola sole} , rappresentare per elencazione e graficamente l’insieme intersezione.
A ∩ B ={s, l, e}
Esercizio n° 2
Dati gli insiemi A = {Carlo, Rita, Paolo, Elena} e B = {Andrea, Franca, Veronica, Elisabetta}, rappresentare per elencazione e graficamente l’insieme intersezione.
Poichè A e B non hanno alcun elemento in comune sono disgiunti, sarà A ∩ B = ∅.
Esercizio n° 3
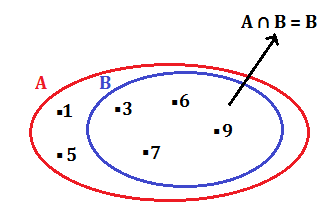
Dati gli insiemi A = {a / a è una cifra del numero 135679} e B = {b / b è una cifra del numero 6793}, rappresentare per elencazione e graficamente l’insieme intersezione.
Poichè B ⊂ A, sarà: A ∩ B = B
Esercizio n° 4
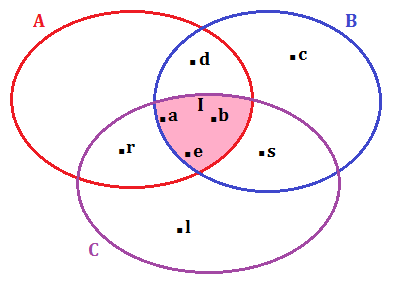
Dati gli insiemi A = {a, b, e, d, r} ; B = {a, b, e, c, d, s} ; C = {a, b, e, s, r, l}, rappresentare per elencazione e graficamente l’insieme intersezione.
Per determinare A ∩ B ∩ C dobbiamo calcolare prima A ∩ B:
A ∩ B = {a, b, e, d} che chiameremo insieme D;
D ∩ C = {a, b, e}
quindi: A ∩ B ∩ C = {a, b, e} che chiameremo insieme F
Esercizio n° 5
Siano A={1,3,5} e B= {2,4}: determinare A ∩ B.
A∩B=∅
Esercizio n° 6
Siano A={a, b, c}, B= {a, d}, C= {c, a}. Rappresentare (A ∩ B) ∩ C e A ∩ (B∩ C).
(A ∩ B) ∩ C= {a}
A ∩ (B∩ C) = {a}
Esercizio n° 7
Sia : A = {a, b, c, d}; B= {a, b, m, n}; indicare gli insiemi A ∩ B; (A ∩ B) ∩ A; (A ∩ B)∩ B.
A ∩ B= {a, b}
(A ∩ B) ∩ A= {a, b}
(A ∩ B)∩ B= {a, b}
Esercizio n° 8
Rappresentare l’insieme unione dell’insieme dei numeri dispari formati da una sola cifra con l’insieme dei numeri pari minori di 10.
A= {1, 3, 5, 7, 9} B= {0, 2, 4, 6, 8}
A∪ B= {0,1, 2,3,4, 5, 6,7,8, 9}
Esercizio n° 9
Rappresentare graficamente gli insiemi A= {m, n, p, q}, B= {m, p, r}, A∪ B, A ∩ B.
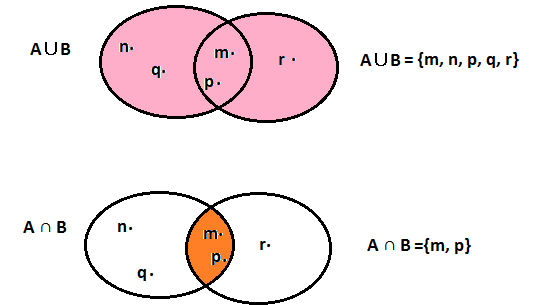
Esercizio n° 10
Siano A= {x|x < 6, x ∈ N} e B = {x|x ≤ 6 x ≤ 7, x ∈ N}; determinare A∪ B e A ∩ B.
A= {0,1, 2, 3, 4, 5} B= {6, 7}
A∪ B= {0,1, 2, 3, 4, 5, 6, 7}
A ∩ B= {ø}
Esercizio n° 11
Consideriamo gli insiemi : A= {1, 2, 3}, B= {2, 4, 6}, C= {1, 3, 5} .
Determinare: A∪ B, B∪C, A∪( B∪C), (A∪ B)∪C, A ∩ B, B ∩ C, A ∩ ( B ∩ C), (A ∩ B)∩ C.
A∪ B= {1, 2, 3, 4, 6}
B∪C={1, 2, 3, 4, 5, 6}
A∪( B∪C)= {1, 2, 3, 4, 5, 6}
(A∪ B)∪C= {1, 2, 3, 4, 5, 6}
A ∩ B= {2}
B ∩ C= {ø}
A ∩ ( B ∩ C)= {ø}
(A ∩ B)∩ C= {ø}
Esercizio n° 12
Determina l’intersezione e l’unione dei due insiemi:
A= {x|x è una lettera della parola “mare”}
B= = {x|x è una vocale}
Con la rappresentazione tabulare avremo:
A= {m, a, r, e} B= {a, e, i, o, u}
A∪ B= {m, a, r, e, i, o, u}
A ∩ B= {a, e}
Esercizio n° 13
Per ogni coppia di insiemi determina l’unione e l’intersezione, rappresentandole con diagramma di Eulero-Venn
A= {2, 5, 7, 12} B= {2, 3, 7, 11, 13}
C={7, 3, 2} D = {2, 3, 7, 11, 13}
E={17, 19, 23} F= {2, 3, 7, 11, 13}
G= {x|x è una lettera della parola “ventilatore”} H= {x|x è una lettera della parola “turbina”}
Esercizio n° 14
Determina l’intersezione e l’unione fra i seguenti insiemi di persone A e B.
A= {x|x ha una statura superiore a 1,30 m} B= {x|x ha una statura inferiore a 1,90 m}
A∪ B= {x|x ha una statura superiore a 1,30 m e 1,90}
A ∩ B= {x|x ha una statura superiore a 1,30 m e 1,90}
A= {x|x ha più di 20 anni} B= {x|x ha meno di 20 anni}
A∪ B= {x|x ha un’età da zero all’infinito}
A ∩ B= {ø}
Esercizio n° 15
Fornisci due esempi di insiemi disgiunti e rappresentali con diagrammi di Eulero-Venn.
A= {x|x ∈ P numeri pari maggiori di 10} B= {x|x ∈ P numeri pari maggiori di 10}
C= {x|x vocali dell’alfabeto} D= {x|x consonanti dell’alfabeto}
Esercizio n° 16
Dati gli insiemi: A= {1, 2, 3, 4, 5}, B= {3, 4, 5, 6, 7}, C= {2, 4, 6, 8} .
Calcoliamo A∪( B∩C), (A∩B)∪C, A∩( B∩C), A∪( B∪C), (A∩B)∩C, (A∪B)∩C.
A∪( B∩C)
Calcoliamo prima ( B∩C)= {4, 6} poi tale insieme lo uniamo con A e quindi avremo:
A∪( B∩C)= {1, 2, 3, 4, 5, 6}
(A∩B)∪C
(A∩B)={ 3, 4, 5} (A∩B)∪C= {2,3, 4, 5, 6, 8} .
A∩( B∩C)
B∩C= { 4, 6} A∩( B∩C)= { 4}
A∪( B∪C)
B∪C= {2, 3, 4, 5, 6, 7, 8} A∪( B∪C)= {1, 2, 3, 4, 5, 6, 7, 8}
(A∩B)∩C
A∩B= { 3, 4, 5} (A∩B)∩C= {ø}
(A∪B)∩C
A∪B={1, 2, 3, 4, 5, 6, 7} (A∪B)∩C = {2, 4, 6} .
Esercizio n° 17
Dati gli insiemi : A= {0, 1, a}, B= {1, 2, a, b}, C= {0, 2, 4}, calcola i risultati delle seguenti espressioni.
A∩B∪C, A∪( B∩C), (A∪B)∩ (A∩C), A∪B∪C, (A∩B)∪ (A∩C), (A∪B)∩ (B∪C)
A∩B∪C= {1, a, 0, 2, 4}
A∪( B∩C)= {0, 2, 1, a}
(A∪B)∩ (A∩C)={0}
A∪B∪C ={0, 1, 2, 4, a, b}
(A∩B)∪ (A∩C)= {1, a, 0}
(A∪B)∩ (B∪C)= {1, 2, 0,a, b}
Esercizio n° 18
Esprimi mediante una espressione con l’unione e l’intersezione fra insiemi, la parte colorata in ognuno dei diagrammi delle figure seguenti.