Un poligono può essere rappresentato nel piano cartesiano mediante le coordinate dei suoi vertici insieme nell’ordine in cui devono essere uniti.
TRIANGOLO RETTANGOLO
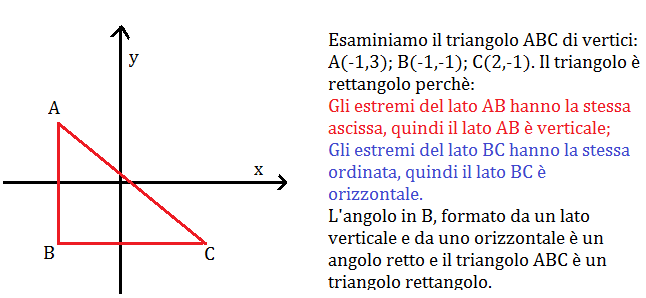
Siamo anche in grado di calcolare il perimetro del triangolo ABC.
AB=.
BC=.
AC=
=
.
Il perimetro sarà AB+BC+AC= 4+3+5=12.
TRIANGOLO ISOSCELE
Calcolando la lunghezza dei lati di un triangolo è possibile stabilire se è isoscele, scaleno o equilatero.
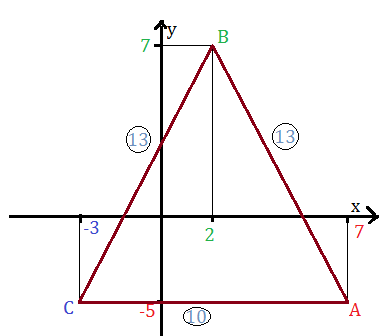
Verifichiamo, che il triangolo ABC di vertici A(7,-5); B(2,7); C(-3,-5) è isoscele, ma non equilatero.
Calcoliamo la lunghezza dei lati:
AB=
;
BC=
=
=
.
I lati AB e BC del triangolo hanno la stessa misura e il triangolo è isoscele.
Per vedere se è anche equilatero calcoliamo la misura dell’ultimo lato.
AC=
La misura di AC è diversa da quella degli altri due lati; quindi il triangolo non è equilatero.
TRAPEZIO
Possiamo anche riconoscere, per esempio un trapezio.
Consideriamo il quadrilatero con vertice nei punti: A(2,3); B(-1,3); C(-2,-1); D(3.5, -1).

RETTANGOLO
Consideriamo il quadrilatero di vertici: A(4,3); B(-2,3); C(-2,-1); (4,-1).
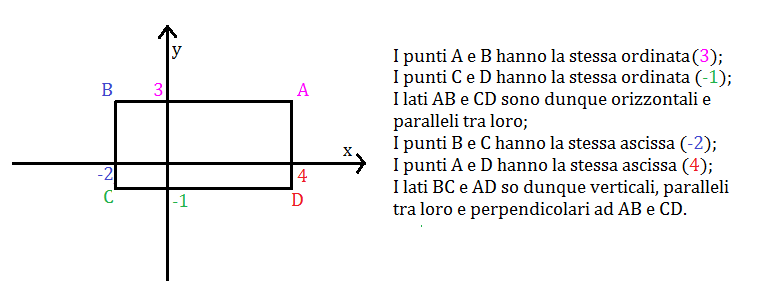
Il quadrilatero ABCD è quindi un rettangolo.
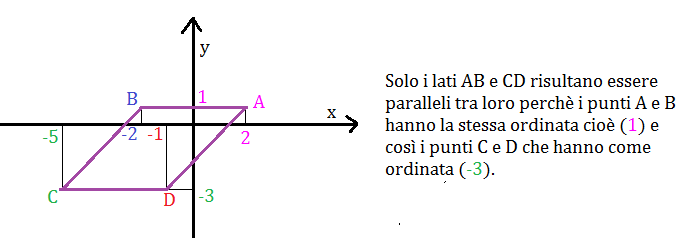
PARALLELOGRAMMA
Esaminiamo il quadrilatero avente per vertici i punti: A(2,1); B(-2,1); C(-5,-3); D(-1,-3).
Calcoliamo le distanze AB e CD:
AB= ;
CD= ;
Quindi AB e CD sono uguali e paralleli, allora i lati BC e AD, che congiungono gli estremi di due segmenti uguali e paralleli, sono a loro volta congruenti e paralleli.
Il poligono è un parallelogramma infatti se facciamo la prova e calcoliamo i lati obliqui vediamo che sono uguali:
BC=
=
;
AD==
.
Problema n° 1
Verifica per ciascun triangolo che è rettangolo e calcolane l’area.
a) Triangolo i cui vertici sono A(- 3 ; -1), B(+5 ; -1), C(-3; +4).
La rappresentazione sul piano cartesiano è:
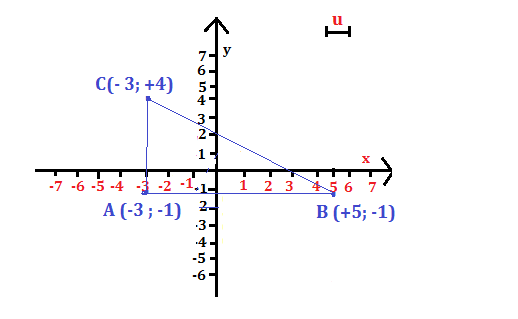
I vertici A e B hanno la stessa ordinata, quindi il lato AB è parallelo all’asse x.
I vertici A e C hanno la stessa ascissa, quindi il lato CA è parallelo all’asse y.
I lati AB e CA sono perpendicolari, per cui il triangolo ABC è rettangolo: AB e CA sono i cateti, BC è l’ipotenusa.
Svolgimento
L’area si ottiene applicando la formula : A =
AB =
= 8u
CA = = 5u
quindi: A = u² = 20 u²
b) Triangolo i cui vertici sono A(-1; -2), b (+9; -2), C(+7; +2).
La rappresentazione sul piano cartesiano è:
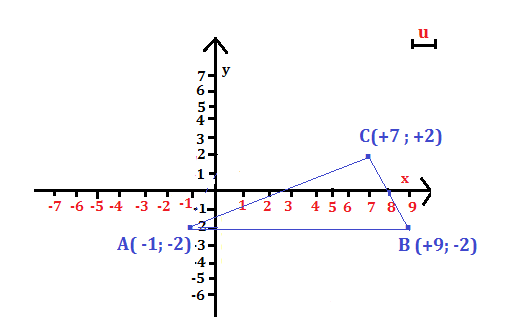
Non essendoci due lati paralleli agli assi, si calcolano le lunghezze dei lati e si verifica se formano una terna pitagorica. Si ottiene:
AB =
BC = =
=
=
= =
CA = =
=
=
= =
I quadrati delle lunghezze dei lati sono AB² = 100 u²; BC² = 20 u²; CA = 80 u²
100 u² = (20 + 80) u², cioè AB² = BC² + CA²
Il triangolo è rettangolo: AB è l’ipotenusa, mentre BC e CA sono i cateti, quindi A= , per cui:
A = u² =
u² =
= 20 u²
Problema n° 2
Verifica che il triangolo di vertici A(+4; 0), B(0; +3), C(+1; -4) è isoscele.
La rappresentazione sul piano cartesiano è:
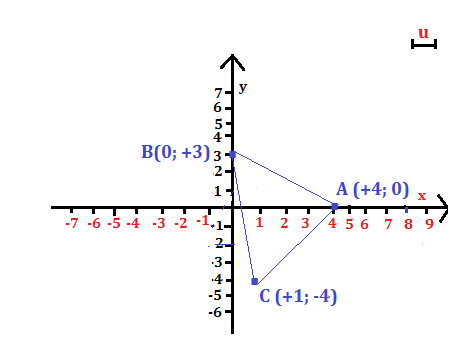
Le lunghezze dei lati sono:
AB = =
=
=
= 5 u
BC = =
=
=
=
CA = =
=
=
=
= 5u
AB = CA = 5 u quindi il triangolo è isoscele.
Problema n° 3
Calcola l’area di un triangolo avente uno dei lati parallelo a un asse.
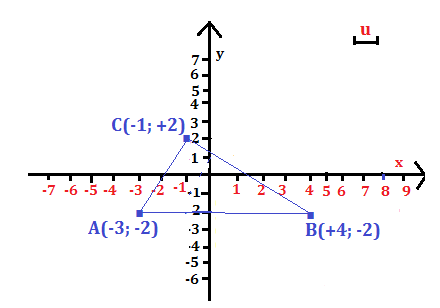
Il lato AB è parallelo all’asse x.
Assumendo AB come base, l’altezza relativa è CH, com H (-1; -2)
La lunghezza della base è:
AB = = 7u
La lunghezza dell’altezza è:
CH = = 4u
A = u² = 14 u²
Problema n° 4
Riconosci la figura rappresentata sul piano cartesiano e calcolane il perimetro e l’area.
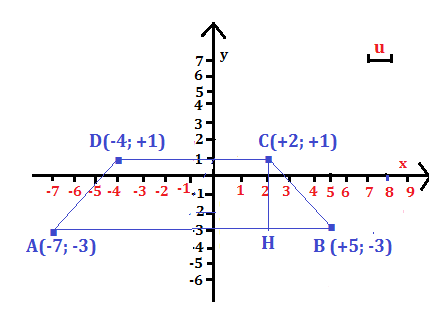
AB =
BC = =
=
=
CD =
DA = =
=
=
I lati AB e CD, paralleli all’asse delle ascisse x, sono paralleli tra loro; i lati BC e DA sono congruenti.
Il quadrilatero ABCD è un trapezio isoscele, per cui:
2p = (12 + 5 + 6 + 5) u = 28 u
L’altezza CH ha per estremi i punti C (+2; +1) e H (+2; -3) quindi:
CH =
A= u² = 36 u²
Problema n° 5
Rappresenta in un piano cartesiano la circonferenza di centro C (+3; +2), passante per ilo punto A(+5; -1) e calcola l’area del cerchio.
Per disegnare la circonferenza con un compasso si fa centro in C e con apertura CA si traccia la circonferenza. La rappresentazione è:
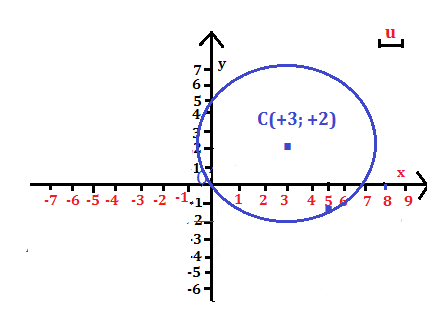
La misura del raggio è:
CA = =
=
= =
=
quindi l’area del cerchio è:
A = π · u² = 13π u²