Il teorema di Pitagora in formule

IL TEOREMA DI PITAGORA IN FORMULE

Il teorema di Pitagora ci consente di affermare che in un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei due quadrati costruiti sui cateti.

da cui si ricava a= che consente di calcolare la lunghezza dell’ipotenusa quando sono note quelle dei cateti.

E’ possibile calcolare anche le due formule inverse:

b²= a²- c²               c²= a²-b²    da cui  ricaviamo:

           che ci consentono di calcolare la lunghezza di un cateto quando sono note le lunghezze dell’ipotenusa e dell’altro cateto.

Problema 

In un triangolo rettangolo i cateti misurano 4 cm e 3 cm . Calcola la misura dell’ipotenusa.

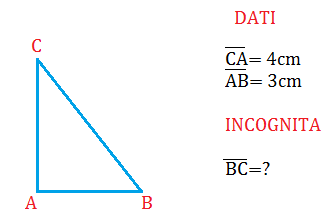
SVOLGIMENTO

Vedi gli esercizi

Programma geometria seconda media