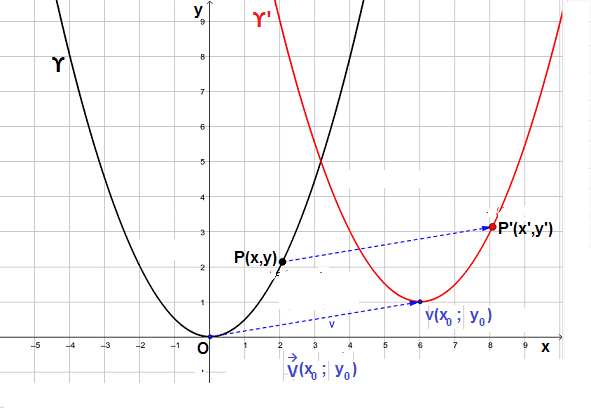
Consideriamo una parabola con asse di simmetria parallelo all’asse y e con vertice non nell’origine degli assi ma in un punto V().
Prendiamo una parabola ϒ con vertice nell’origine e otteniamo un’altra parabola ϒ’ traslata rispetto a ϒ e ad essa congruente.
La parabola ϒ poichè ha vertice nell’origine O(0,0) e asse di simmetria coincidente con l’asse y, avrà l’equazione y=ax². Sottoponendo i punti di questa parabola a una traslazione di vettore , otteniamo la parabola ϒ’ con vertice
Le equazioni della traslazione saranno:
esplicitando la x otteniamo:
l’equazione di ϒ è y=ax². , la sostituzione che dobbiamo fare in questa equazione è :
e
.
A questo punto per ottenere l’equazione della parabola ϒ’ sostituiamo alla parabola ϒ e cioè a y=ax² i dati ottenuti dalla traslazione ottenendo:
ovviamente gli apici delle variabili, quindi di x e di y servono solo a distinguerli tra le due parabole , quindi l’equazione ottenuta lai si può scrivere anche come:
Quindi in definitiva una parabola con asse parallelo all’asse y e vertice nel punto ha l’equazione nella forma
con a≠0
Pero l’equazione conosciuta e che usiamo negli esercizi la otteniamo esplicitando la y e svolgendo dei calcoli. Vediamo cosa fare:
poniamo e
ottenendo così :
equazione della parabola con asse parallelo all’asse y.
Dalla seguenti equazioni e
possiamo ricavare :
Quindi il vertice ha come coordinate
L’asse di simmetria ha equazione
Usando la traslazione e partendo dalla parabola ϒ e quindi dal suo fuoco otteniamo :
il fuoco che è:
La direttrice sarà
Per quanto riguarda la concavità della parabola essa dipende dal valore della a , quindi:
- se a>0, la parabola volge la concavità versi l’alto;
- se a<0 la parabola volge la concavità verso il basso.
Quindi quanti più a in valore assoluto è piccolo, tanto più la parabola è aperta , quanto più è grande , tanto più la parabola è chiusa.
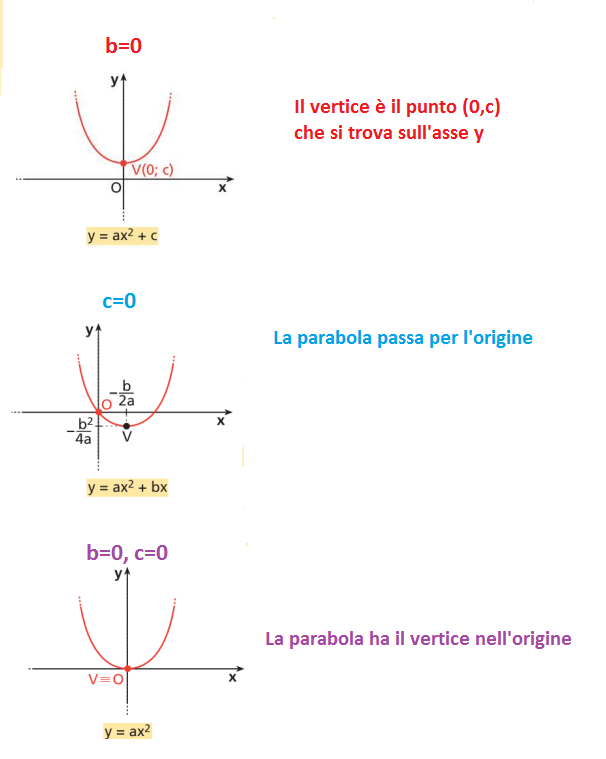
Per quanto riguarda il grafico della parabola anche il valore di b e il valore di c lo influenzano.