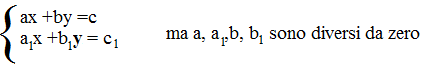Prima di svolgere qualsiasi sistema, una volta che è ridotto in forma normale, si può verificare già il numero di soluzioni , quindi si può dire se il sistema è determinato, cioè con un numero finito di soluzioni, indeterminato, quando il numero di soluzioni è infinito e impossibile, quando non ci sono soluzioni.
Nello specifico in un sistema determinato e lineare esiste una sola soluzione.
Consideriamo un sistema generico:
Tale sistema è determinato quando il rapporto tra i coefficienti di x e cioè è diverso dal rapporto tra i coefficienti di y e cioè
e quello dei termini noti
quindi :
Graficamente un sistema determinato potrà essere rappresentato come due rette che si incontrano in un punto.
Un sistema è indeterminato quando ha infinite soluzioni, quindi come risultato di un’equazione del sistema ci troveremo 0=0.
Se consideriamo un generico sistema, scritto in forma normale:
esso sarà indeterminato quando il rapporto tra i coefficienti di x e cioè è uguale al rapporto tra i coefficienti di y e cioè
ed è anche uguale al rapporto fra i termini noti
quindi :
Graficamente le rette di un sistema indeterminato coincidono.
Un sistema è impossibile quando non ammette soluzioni, quindi ci troveremo almeno un’equazione con un risultato assurdo come, 0= 6.
Consideriamo sempre il sistema generico, messo in forma normale:
E’ impossibile quando il rapporto tra i coefficienti di x e cioè è uguale al rapporto tra i coefficienti di y e cioè
ed è diverso dal rapporto fra i termini noti
quindi :
Graficamente un sistema del genere verrà rappresentato con due rette parallele che quindi non si potranno mai incontrare.
Vedi gli esercizi
Vedi programma di matematica del secondo superiore