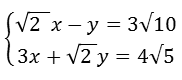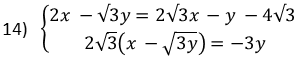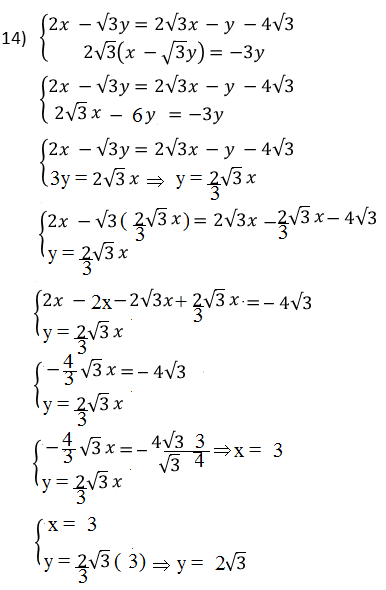Esercizi sulle equazioni con i radicali
1)
2)
3)
4)
5)
6)
Esercizi sulle equazioni fratte con i radicali
7)
8)
Disequazioni con i radicali
9)
10)
11)
Sistemi con i radicali
13)
Svolgimento
1)
Razionalizziamo
2)
(ricorda che moltiplicando due radici identiche il risultato è il radicando cioè il numero sotto la radice
razionalizziamo
3)
x² va via e
razionalizziamo
4)
il denominatore lo possiamo semplificare moltiplicando entrambi i membri per lo stesso valore
razionalizziamo
5)
6)
le x² vanno via
razionalizziamo
7)
C.E. quindi
quindi
razionalizziamo
questa soluzione è accettabile perchè è diversa dalla condizione d’esistenza
8)
= 0
C.E.
;
;
le x² vanno via
La soluzione non è accettabile perchè uguale alla condizione d’esistenza quindi l’equazione è impossibile
9)
il denominatore essendo numerico lo possiamo far andare via
10)
Il denominatore può andare via e cambiamo il segno della disequazione perchè stiamo moltiplicando per una quantità negativa
razionalizziamo
11)
moltiplichiamo entrambe i membri per il denominatore e invertiamo il segno in quanto stiamo moltiplicando per una quantità negativa
13
e
risultato:x = 3 ;