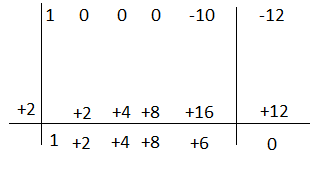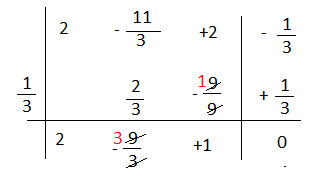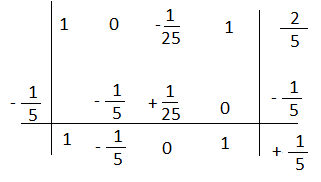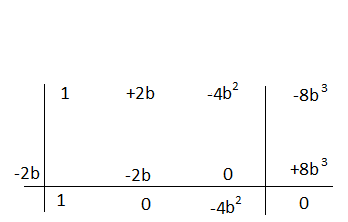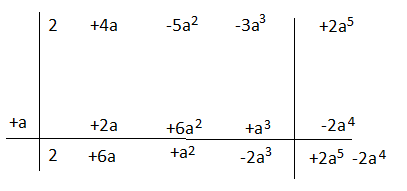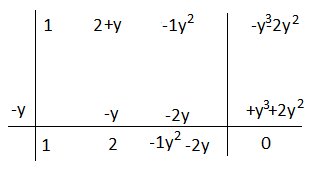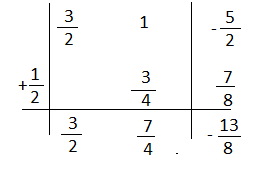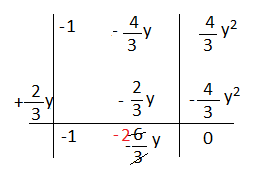Esercizi sulle divisioni con Ruffini
Esercizio n° 1
Esegui la seguente divisione applicando Ruffini.
(2x³ + 3x – 8): (x +2)
Esercizio n° 2
Esegui la seguente divisione applicando Ruffini.
(b³ + b² – b + 15) : (b + 3)
Esercizio n° 3
Esegui la seguente divisione applicando Ruffini.
( -10a -12) : (a -2)
Esercizio n° 4
Esegui la seguente divisione applicando Ruffini.
Esercizio n° 5
Esegui la seguente divisione applicando Ruffini.
Esercizio n° 6
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(a³ +2a²b – 4ab² – 8b³) : (a + 2b)
Esercizio n° 7
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(2 – 5a²x² + 4ax³ -3a³x +2
) : (x-a)
Esercizio n° 8
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(x³ – xy² + x²y – y³ +2x² – 2y² ) . (x + y)
Esercizio n° 9
Calcola il quoziente e il resto della divisione. mediante la regola di Ruffini.
(3a² + 2a – 5) : (2a – 1)
Esercizio n° 10
Calcola il quoziente e il resto della divisione mediante la regola di Ruffini.
(-3x² -4xy + 4y²) : (3x – 2y)
Esercizio n° 11
Calcola il quoziente e il resto della divisione mediante la regola di Ruffini.
(5a³ + 1\4a²+13\12a +1\3) . (2a + 1\2)
Svolgimento
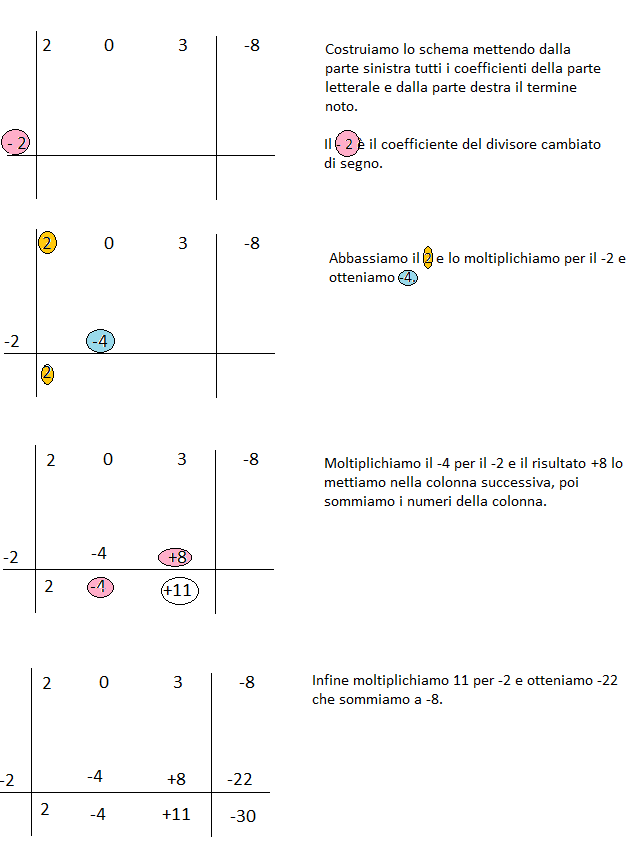
Esercizio n° 1
Esegui la seguente divisione applicando Ruffini.
(2x³ + 3x – 8): (x +2)
Poichè il dividendo è di terzo grado, il polinomio risultante sarà di secondo grado: 2x² -4x +11 con resto di -30
Esercizio n° 2
Esegui la seguente divisione applicando Ruffini.
(b³ + b² – b + 15) : (b + 3)
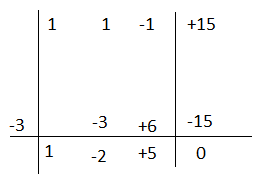
Il quoziente è b² -2b +5
Esercizio n° 3
Esegui la seguente divisione applicando Ruffini.
( -10a -12) : (a -2)
Il quoziente è +2a³ +4a² + 8a +6
Esercizio n° 4
Esegui la seguente divisione applicando Ruffini.
(2b³ – 11\3b² – 1\3 + 2b) : (b – 1\3)
Bisogna ricordarsi di mettere in ordine decrescente secondo gli esponenti della parte letterale.
Il quoziente è 2b² – 3b + 1
Esercizio n° 5
Esegui la seguente divisione applicando Ruffini.
Il quoziente è a³ -1\5 a² + 1 con resto 1\5
Esercizio n° 6
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(a³ +2a²b – 4ab² – 8b³) : (a + 2b)
Il quoziente è a² -4b²
Esercizio n° 7
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(2 – 5a²x² + 4ax³ -3a³x +2
) : (x-a)
Mettendo in ordine secondo gli esponenti della x avremo: 2+ 4ax³- 5a²x² -3a³x+2
Il quoziente è 2x³ +6ax² +a²x -2a³ il resto è
Esercizio n° 8
Esegui la seguente divisione applicando Ruffini considerando come variabile la prima lettera che compare nel dividendo.
(x³ – xy² + x²y – y³ +2x² – 2y² ) :(x + y)
Mettendo in ordine secondo gli esponenti della x avremo: x³ + 2x² + x²y – xy²- y³ – 2y²
Il quoziente è x² +2x -y² -2y
Esercizio n° 9
Calcola il quoziente e il resto della divisione. mediante la regola di Ruffini.
(3a² + 2a – 5) : (2a – 1)
Per poter svolgere questa divisione dobbiamo ricordare che se in una divisione dividiamo sia il dividendo che il divisore per uno stesso numero, anche il resto viene diviso per lo stesso numero mentre il quoziente non cambia, quindi alla fine dell’operazione dobbiamo moltiplicare il resto per 2.
Quindi nel nostro caso dividiamo tutto per 2 in modo da togliere il coefficiente dalla parte letterale del divisore.
Il quoziente è : ; invece il resto si ottiene moltiplicando per 2 il resto
, avremo:
Esercizio n° 10
Calcola il quoziente e il resto della divisione mediante la regola di Ruffini.
(-3x² -4xy + 4y²) : (3x – 2y)
Dividiamo tutto per 3 cioè il coefficiente della x del divisore e avremo:
Il quoziente è : -x -2y
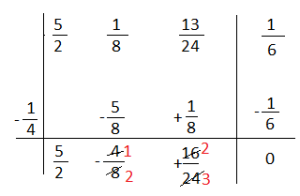
Esercizio n° 11
Calcola il quoziente e il resto della divisione mediante la regola di Ruffini.
(5a³ + 1\4a²+13\12a +1\3) . (2a + 1\2)
Dividiamo tutto per 2 cioè il coefficiente della a del divisore e avremo: