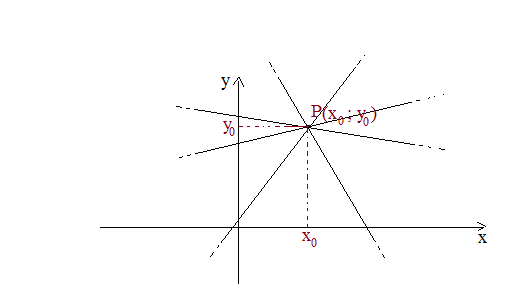
Vediamo cosa dobbiamo fare se vogliamo scrivere l’equazione di una retta di cui conosciamo il punto attraverso cui passa P(;
) e il coefficiente angolare m.
Sappiamo che l’equazione generale di una retta è y = mx + q. Se consideriamo che il punto P passa per questa retta , le sue coordinate devono soddisfare l’equazione della retta quindi avremo che: =m
+ q.
Dalla seconda equazione esplicitiamo la q e l’andiamo a sostituire nella prima. Quindi:
q= – m
andando a sostituire avremo:
y = mx + – m
⇒
quindi è l’equazione di una retta passante per un punto noto e coefficiente angolare conosciuto.
Tale equazione viene anche detta equazione del fascio di rette di centro P(
:
). Quindi al variare di m si ottengono le infinite rette che passano per il punto P. Esso può essere definito anche fascio proprio in quanto il fascio improprio è l’insieme di rette tutte parallele tra loro.
Vediamo ora alcuni esempi di esercizi.
1) Data la retta r di equazione 2x – y + 3= 0, scrivi l’equazione della retta parallela a r e passante per il punto A(4,3).
La prima cosa da fare è scrivere l’equazione in forma esplicita y=2x + 3. Notiamo che il coefficiente angolare è 2, anche dalla forma implicita si poteva calcolare la m che è uguale a -a\b che veniva sempre = 2. Poichè la retta è parallele per la condizione di parallelismo il coefficiente angolare è lo stesso.
Una volta individuato il coefficiente angolare si può calcolare con la formula del fascio di rette , dove
e
sono le coordinate del punto A.
Quindi y – 3 = 2(x – 4) ⇒ y = 3 + 2x – 8 ⇒ y = 2x – 5
2)Data la retta 5 di equazione 3x + y – 2= 0, scrivi l’equazione della retta perpendicolare e passante per il punto B(0; -3)
Prima di tutto mettiamo in forma esplicita l’equazione: y = -3x + 2.
Il coefficiente angolare sappiamo che dovrà essere m’ = – 1\m ⇒ m’ = + 1\3
Applichiamo ora la formula avremo y +3 = 1\3(x – o) ⇒ y = 1\3x – 3