Un retta che non passa per l’origine avrà equazione y=mx+q dove m è il coefficiente angolare e q è il termine noto ed è l’ordinata del punto d’intersezione della retta con l’asse delle y.
m e q sono quindi dei numeri reali.
Se q=0 la retta passa per l’origine degli assi.
Per disegnare una retta non passante per l’origine, poichè per due punti passa una sola retta, si possono trovare le coordinate solo dei due punti.
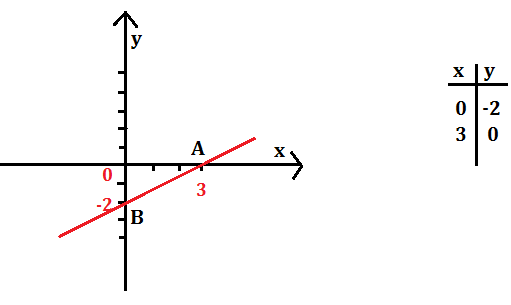
Ad esempio volendo disegnare la retta di equazione y=2\3 x -2 si fa uno schemino e si attribuiscono ad x dei valori a cui corrisponderanno determinati valori di y.
Avremo cioè i punti A(0,-2); B(+3,0) ed il diagramma sarà la retta AB.
Spesso per una maggiore precisione del disegno si possono cercare anche altri punti.
Le rette in forma esplicita sono quelle scritte appunto come y = mx + q con m e q ∈R; per esempio y = 1\2x + 2. La retta scritta in questa maniera rappresenta tutte le rette del piano escluso l’asse y e le parallele ad esso. Infatti, non esistono valori di m e di q che, sostituiti nell’equazione, ci forniscano equazioni del tipo x=0 e x= k.
Un’equazione che può rappresentare tutte le rette del piano si dice che è in forma implicita cioè ax +by + c = 0 con a,b,c ∈ R. Quindi per esempio una retta in forma implicita è 4x + 2y + 7 = 0.
Se abbiamo un’equazione si può passare tranquillamente da una forma all’altra. Per esempio possiamo passare da un’equazione in forma implicita ad una in forma esplicita, purchè b≠0 ax + by +c =0 , infatti per eliminare la b da vicino alla y dividiamo tutti i membri per b e otteniamo:
Facciamo un esempio:
consideriamo l’equazione della retta 6x – 2y + 1 = 0 scritta in forma implicita e trasformiamola in forma esplicita. Lasciamo la y da una parte e trasportiamo il resto dall’altra -2y = -6x – 1⇒ 2y = 6x + 1 . A questo punto dividiamo tutto per due in modo da togliere il coefficiente numerico da vicino alla y. Otteniamo:
Possiamo infine affermare che le equazioni lineari di primo grado in due variabili, poichè rappresentano le rette del piano cartesiano, vengono chiamate equazioni lineari. Ogni punto appartiene a una retta se le sue coordinate soddisfano l’equazione della retta, cioè se i valori del punto una volta sostituiti nella retta soddisfano l’equazione della retta.