Rette parallele all’asse y
RETTE PARELLELE ALL’ASSE Y
Le rette parallele all’asse y sono caratterizzate dall’avere tutti i punti con coordinate del tipo (a;y) dove a è una costante, che indica la posizione della retta rispetto all’asse y, mentre y varia nell’insieme dei numeri reali.
Questo significa che, se due punti hanno la stessa ascissa a, allora appartengono a una stessa retta parallela all’asse delle ordinate.
ESEMPIO
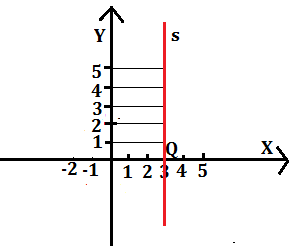
- Consideriamo una retta s parallela all’asse y che incontra l’asse x nel punto Q di ascissa +3. Poichè tutti i punti di s hanno uguale distanza dall’asse y, cioè hanno l’ascissa x=+3, diciamo che x=3 è l’equazione della retta parallela all’asse y.
- Se consideriamo una retta s che coincide con l’asse y, la sua distanza dall’asse y è d=0 e la sua equazione x=0.
- Se consideriamo una retta t parallela all’asse y la sua distanza dall’asse y è d= | -3| e la sua equazione è x= -3
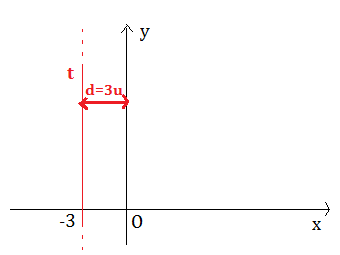
L’equazione di una retta parallela all’asse delle y è del tipi x = k dove k indica l’ascissa di tutti i punti della retta:
- se k > 0 la retta giace nel I e nel IV quadrante;
- se k < 0 la retta giace ne II e nel II quadrante;
- se k = 0 la retta coincide con l’asse y e x = 0 è l’equazione dell’asse y.
Esercizio
Con riferimento alla figura, esegui quanto indicato.
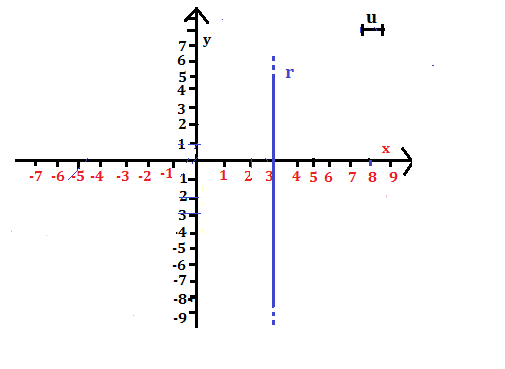
a) Scrivi le coordinate di tre punti A, B, C, appartenenti alla retta r e aventi le ordinate rispettivamente uguali a – 7, -1 +5.
Tutti i punti della retta r hanno l’ascissa uguale a +3, quindi i punti sono:
A (+3; -7), B (+3; -1), C (+3; +5)
b) Scrivi l’equazione della retta r. L’equazione della retta r è : x = +3
c) Indica i quadranti su cui giace la retta r.
La retta r giace sul I e IV quadrante
d) Indica la distanza tra la retta r e l’asse y.
La distanza è : d= |+3| = 3u