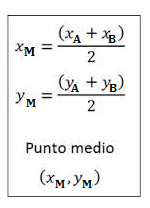
Il punto medio M del segmento AB , è quel punto che divide AB in due parti uguali, quindi le coordinate del punto M si trovano con la formula della media aritmetica;
l’ascissa del punto medio è data dalla semisomma delle ascisse degli estremi A e B; l’ordinata si otterrà come semisomma dell’ordinata degli estremi AB.
Geometria analitica
ESEMPIO
Determinare le coordinate del punto medio M del segmento PQ in cui: P(3,2) e Q(5,8).
Si ha:
Esercizio n° 1
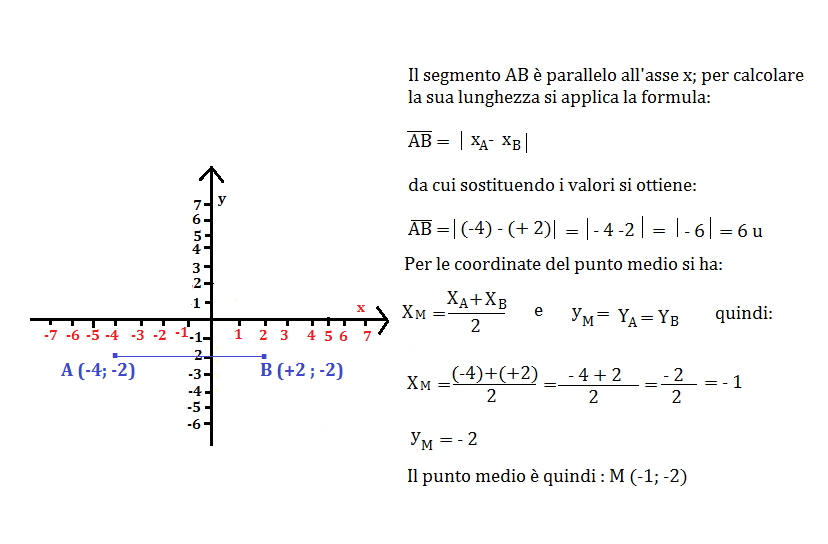
Determina la lunghezza e le coordinate del punto medio di un segmento parallelo all’asse x.
Esercizio n° 2
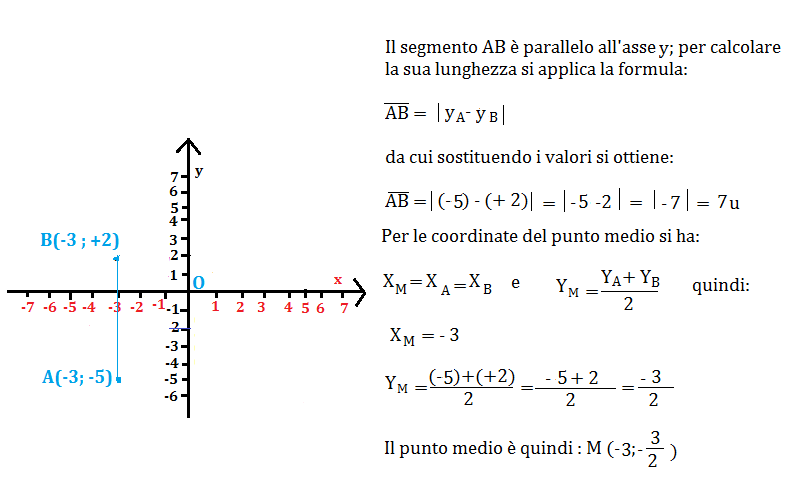
Determina la lunghezza e le coordinate di M di un segmento parallelo all’asse y.
Esercizio n° 3
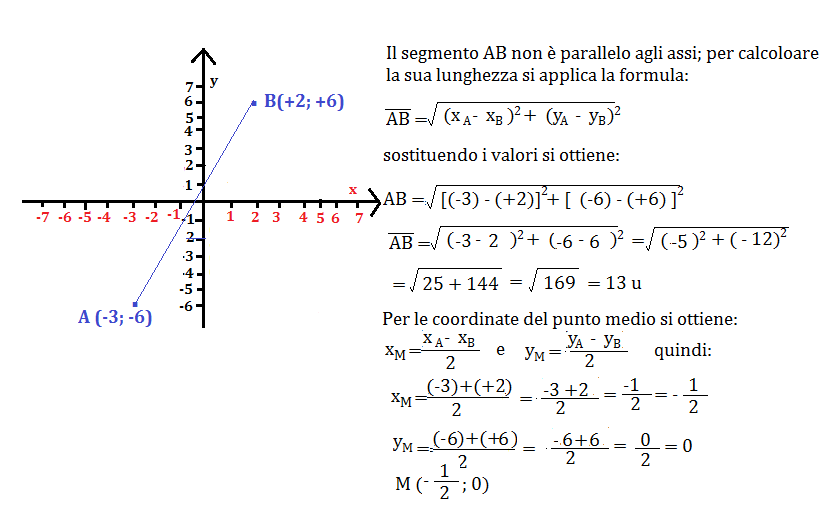
Determina la lunghezza di un segmento AB non parallelo agli assi e le coordinate del suo punto M.
Se il segmento è posto in orizzontale o in verticale, sarà semplice calcolarlo graficamente, contando semplicemente i quadratini che dividono il segmento in due parti uguali,