RETTE PERPENDICOLARI TRA LORO
Due rette perpendicolari sono caratterizzate dal fatto che, se una ha il coefficiente angolare m, l’altra ha come coefficiente angolare -1\m ovvero l’opposto del reciproco della prima.
Sono perpendicolari fra loro:
y=-3x+2 e
perchè della prima retta m=-3 invece della seconda m =+1\3
Possiamo allora dedurre che due rette che per coefficienti angolari hanno due numeri relativi opposti e reciproci sono perpendicolari. (condizione di perpendicolarità)
Data la retta r: y = mx + q e la retta s: y = m’x + q’
r⊥s se e solo se: m = – 1\m, oppure m · m’= -1
Esercizio
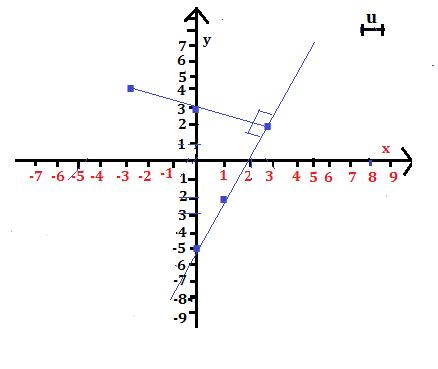
Rappresenta in un sistema di assi cartesiani la retta di equazione y = +3x -5 e disegna la retta a essa perpendicolare e passante per il punto P (0; +3). Qual è la sua equazione?
La retta y = +3x -5 ha coefficiente angolare m = +3 e quindi la retta ad essa perpendicolare avrà coefficiente angolare uguale a –-1\m quindi: m’ = -1\3
Visto che la seconda retta dovrà passare per il punto P, sostituiamo tutti i dati conosciuti nell’equazione y = m’x + q.
L’equazione della seconda retta sarà:
La tabella dei valori per y = +3x -5 sarà:
| x | +1 | 0 | -1 |
| y | -2 | -5 | -6 |
Quindi la retta passera per i punti A (+1; -2), B (0; -5), C (-1; -6).
La tabella dei valori per sarà:
| x | -3 | 0 | +3 |
| y | +4 | +3 | +2 |
Quindi la retta passera per i punti D( -3 ; +4), E (0 ; +3), F (+3 ; +2)