Esercizio di geometria solida
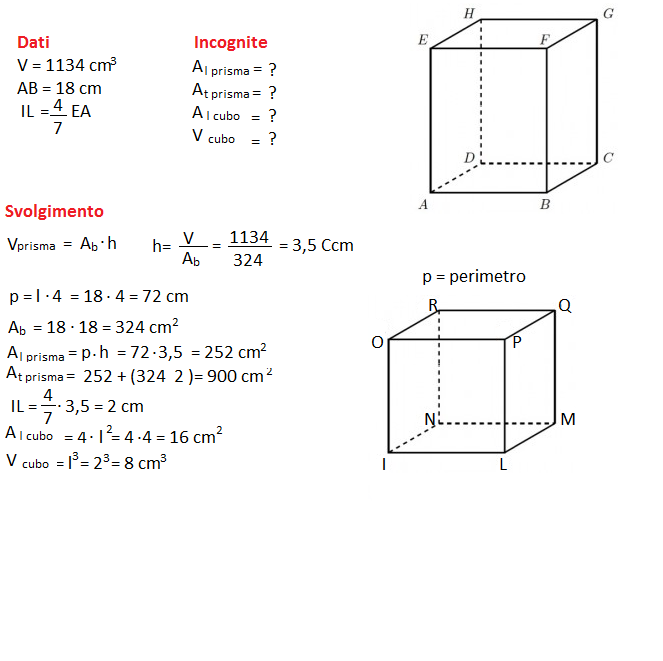
Il volume di un prisma regolare quadrangolare è 1134 cm³ e lo spigolo di base misura 18 cm. Calcola:
- l’area laterale e l’area totale del prisma
- l’area laterale e il volume di un cubo che ha lo spigolo congruente a 4\7 dell’altezza del prisma.
Equazione
Spiega con alcuni esempi che cosa significa che un’equazione è determinata, indeterminata o impossibile. Risolvi la seguente equazione e specifica di quale dei tre tipi si tratta.
Esercizio sul piano cartesiano
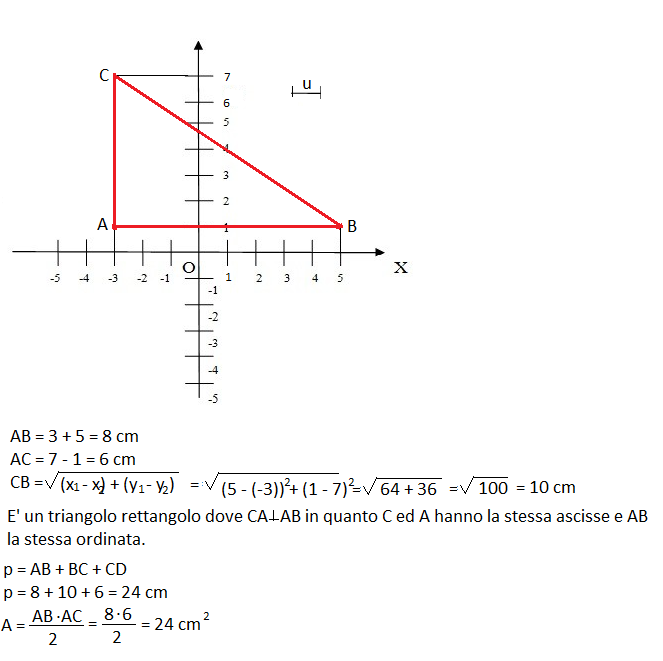
Fissa su un piano cartesiano i punti:
A(-3 ; 1) B(5 ; 1) C(-3,7)
Congiungi i punti A, B e C, descrivi le caratteristiche della figura che hai ottenuto e calcolane il perimetro e l’area (u = 1 cm).
Determinare inoltre l’area laterale, l’area totale e il volume del solido ottenuto facendo ruotare di 360° la figura attorno al lato AB.
Esercizio sulla probabilità
In un cassetto ci sono 15 magliette: 5 verdi, 7 rosse e 3 gialle.
Prendendo a caso una maglietta, cioè senza guardare, indica quale dei seguenti eventi è certo, probabile o impossibile.
E(1) :”prendere una maglietta azzurra”;
E(2): “prendere una maglietta di colore verde”;
E(3): “prendere una maglietta verde o rossa o giallo”.
Calcola ora la probabilità che venga presa:
- una maglietta gialla
- una gialla o rossa
- una rossa o verde
Svolgimento
Esercizio di geometria solida
Il volume di un prisma regolare quadrangolare è 1134 cm³ e lo spigolo di base misura 18 cm. Calcola:
- l’area laterale e l’area totale del prisma
- l’area laterale e il volume di un cubo che ha lo spigolo congruente a 4\7 dell’altezza del prisma.
Equazione
Spiega con alcuni esempi che cosa significa che un’equazione è determinata, indeterminata o impossibile. Risolvi la seguente equazione e specifica di quale dei tre tipi si tratta.
Si possono verificare varie situazioni:
- può capitare che un’equazione non ammetta soluzioni, cioè non esista alcun valore delle incognite che la trasformi in una identità: si dice allora che l’equazione è impossibile. Per esempio sono impossibili le equazioni
5x +3 = 5x + 7 perchè la x va via , infatti si ottiene 0 =4
- Può darsi che un’equazione ammetta un numero illimitato di soluzioni; essa si dice indeterminata. Per esempio l’equazione
3x + 2 =3(x – 2) + 8 ⇒ 3x + 2 = 3x – 6 + 8 il risultato è 0=0 quindi è indeterminata perchè è verificata da tutti gli infiniti valori che si possono attribuire alla x.
- Infine un’equazione, la quale ammette un numero limitato di radici si dice determinata. Per esempio l’equazione
5x – 6= 3x – 2 ⇒ 2x = 4 ⇒ x = 2 quindi questa è l’unica soluzione ammessa dall’equazione.
-5x -5 +9x +18 = -2x+4 +18x -12x -24
-5x +9x +2x -18x +12x = +4 -24 +5 -18
0= -33
Esercizio sul piano cartesiano
Fissa su un piano cartesiano i punti:
A(-3 ; 1) B(5 ; 1) C(-3,7)
Congiungi i punti A, B e C, descrivi le caratteristiche della figura che hai ottenuto e calcolane il perimetro e l’area (u = 1 cm).
Determinare inoltre l’area laterale, l’area totale e il volume del solido ottenuto facendo ruotare di 360° la figura attorno al lato AB.
La figura che si ottiene dalla rotazione del triangolo attorno ad AB è un cono che avrà :
apotema = BC = 10 raggio = AC= 6 cm altezza = AB = 8 cm
A(l) = π · r · a = π · 6 · 10 = 60 π cm²
A(t) = A(l) + A(b)
A(b) = π · r² = π · 6² = 36π cm²
A(t) =60 + 36 = 96π cm²
Esercizio sulla probabilità
In un cassetto ci sono 15 magliette: 5 verdi, 7 rosse e 3 gialle.
Prendendo a caso una maglietta, cioè senza guardare, indica quale dei seguenti eventi è certo, probabile o impossibile.
E(1) :”prendere una maglietta azzurra”; impossibile
E(2): “prendere una maglietta di colore verde”; probabile
E(3): “prendere una maglietta verde o rossa o giallo” certo
Calcola ora la probabilità che venga presa:
- una maglietta gialla
- una gialla o rossa
- una rossa o verde 12\15=4\5